---
title: "Feynman diagram"
firstLetter: "F"
publishDate: 2021-11-18
categories:
- Physics
- Quantum mechanics
date: 2021-11-15T21:01:46+01:00
draft: false
markup: pandoc
---
# Feynman diagram
When doing calculations in the context of condensed matter physics and quantum field theory,
**Feynman diagrams** graphically represent expressions
that would be tedious or error-prone to work with directly.
This article is about condensed matter physics.
Suppose we have a many-particle Hamiltonian $\hat{H} = \hat{H}_0 + \hat{H}_1$,
consisting of an "easy" term $\hat{H}_0$,
and then a "difficult" term $\hat{H}_1$
with time-dependent and/or interacting parts.
Let $\ket{\Phi_0}$ be a known eigenstate (or superposition thereof)
of the easily solvable part $\hat{H}_0$,
with respect to which we will take expectation values $\expval{}$.
Below, we go through the most notable components of Feynman diagrams
and how to translate them into a mathematical expression.
## Real space
The most common component is a **fermion line**, which represents
a [Green's function](/know/concept/greens-functions/) $G^0$
for the simple Hamiltonian $\hat{H}_0$.
Any type of Green's function is possible in theory (e.g. a retarded),
but usually the *causal* function is used.
Let the subscript $I$ refer to the
[interaction picture](/know/concept/interaction-picture/),
and $\mathcal{T}\{\}$ denote the
[time-ordered product](/know/concept/time-ordered-product/):
$$\begin{aligned}
= i \hbar G_{s_2 s_1}^0(\vb{r}_2, t_2; \vb{r}_1, t_1)
= \expval{\mathcal{T} \Big\{ \hat{\Psi}_{s_2 I}(\vb{r}_2, t_2) \hat{\Psi}_{s_1 I}^\dagger(\vb{r}_1, t_1) \Big\}}
\end{aligned}$$
The arrow points in the direction of time, or more generally,
from the point of creation $\hat{\Psi}{}^\dagger$
to the point of annihilation $\hat{\Psi}$.
The dots at the ends are called **vertices**,
which represent points in space and time with a spin.
Vertices can be
**internal** (one Green's function entering AND one leaving)
or **external** (either one Green's function entering OR one leaving).
Less common is a **heavy fermion line**, representing
a causal Green's function $G$ for the entire Hamiltonian $\hat{H}$,
where the subscript $H$ refers to the [Heisenberg picture](/know/concept/heisenberg-picture/):
$$\begin{aligned}
= i \hbar G_{s_2 s_1}(\vb{r}_2, t_2; \vb{r}_1, t_1)
= \expval{\mathcal{T} \Big\{ \hat{\Psi}_{s_2 H}(\vb{r}_2, t_2) \hat{\Psi}_{s_1 H}^\dagger(\vb{r}_1, t_1) \Big\}}
\end{aligned}$$
Next, an **interaction line** or **boson line** represents
a two-body interaction operator $\hat{W}$ (in $\hat{H}_1$),
which we assume to be instantaneous, i.e. time-independent
(in quantum field theory this is *not* assumed),
hence it starts and ends at the same time,
and no arrow is drawn:
$$\begin{aligned}
= \frac{1}{i \hbar} W_{s_2 s_1}(\vb{r}_2, t_2; \vb{r}_1, t_1)
= \frac{1}{i \hbar} W(\vb{r}_2, \vb{r}_1; t_1) \: \delta(t_2 - t_1)
\end{aligned}$$
We have chosen to disallow spin flipping,
so $W$ does not depend on $s_1$ or $s_2$.
For reference, this function $W$
has a time-dependence coming only from the interaction picture,
and is to be used as follows to get the full two-body operator $\hat{W}$:
$$\begin{aligned}
\hat{W}
= \frac{1}{2} \sum_{s_1 s_2} \iint_{-\infty}^\infty \hat{\Psi}_{s_1}^\dagger(\vb{r}_1) \hat{\Psi}_{s_2}^\dagger(\vb{r}_2)
W(\vb{r}_1, \vb{r}_2) \hat{\Psi}_{s_2}(\vb{r}_2) \hat{\Psi}_{s_1}(\vb{r}_1) \dd{\vb{r}_1} \dd{\vb{r}_2}
\end{aligned}$$
One-body (time-dependent) operators $\hat{V}$ in $\hat{H}_1$
are instead represented by a special vertex:
$$\begin{aligned}
= \frac{1}{i \hbar} V_s(\vb{r}, t)
\end{aligned}$$
Other graphical components exist representing
more complicated operators and quantities,
but these deserve their own articles.
In order for a given Feynman diagram to be valid,
it must satisfy the following criteria:
a. Each vertex must be connected to one or two fermion lines,
at most one of which leaves,
and at most one of which enters.
b. Each internal vertex contains at most one "event";
which could be $V$ or $W$.
Finally, we need some additional rules to convert
diagrams into mathematical expressions:
1. Disallow spin flipping by multiplying
each internal vertex by $\delta_{s_\mathrm{in} s_\mathrm{out}}$.
2. If both ends of a line are at the same time (always the case for $W$),
an infinitesimal $\eta \to 0^+$ must be added
to the time of all creation operators,
so e.g. $G(t, t) \to G(t, t\!+\!\eta)$.
3. Integrate over spacetime coordinates $(\vb{r}, t)$
and sum over the spin $s$ of all internal vertices,
but not external ones.
4. Multiply the result by $(-1)^F$,
where $F$ is the number of closed fermion loops.
5. Depending on the context, additional constant factors may be required;
sometimes they are changed on-the-fly during a calculation.
Note that rules 4 and 5 are convention,
just like the factors $i \hbar$ in $G^0$, $G$, $V$ and $W$;
it simply turns out to be nicer to do it this way
when using Feynman diagrams in the wild.
The combination of rules 2 and 3 means that spin
belongs to lines rather than vertices,
so that a particle with a given spin propagates
from vertex to vertex without getting flipped.
## Fourier space
If the system is time-independent and spatially uniform,
meaning it has continuous translational symmetry in time and space,
then it is useful to work in [Fourier space](/know/concept/fourier-transform/):
$$\begin{aligned}
G_{s_2 s_1}^0(\vb{r}_2, t_2; \vb{r}_1, t_1)
&= G_{s_1}^0(\vb{r}_2 - \vb{r}_1, t_2 - t_1) \: \delta_{s_2 s_1}
\\
&= \frac{\delta_{s_2 s_1}}{(2 \pi)^4} \iint_{-\infty}^\infty G_{s_1}^0(\vb{k}, \omega) \:
e^{i \vb{k} \cdot (\vb{r}_2 - \vb{r}_1)} e^{- i \omega (t_2 - t_1)} \dd{\vb{k}} \dd{\omega}
\\
W_{s_2 s_1}(\vb{r}_2, t_2; \vb{r}_1, t_1)
&= W(\vb{r}_2 - \vb{r}_1) \: \delta(t_2 - t_1)
\\
&= \frac{1}{(2 \pi)^4} \iint_{\infty}^\infty W(\vb{k}) \:
e^{i \vb{k} \cdot (\vb{r}_2 - \vb{r}_1)} e^{- i \omega (t_2 - t_1)} \dd{\vb{k}} \dd{\omega}
\end{aligned}$$
Where we have used an integral representation of
the [Dirac delta function](/know/concept/dirac-delta-function/).
Note the inconsistent sign of the exponent
in the Fourier transform definitions for space and time.
Working in Fourier space allows us to simplify calculations.
Consider the following diagram and the resulting expression,
where $\tilde{\vb{r}} = (\vb{r}, t)$, and $\tilde{\vb{k}} = (\vb{k}, \omega)$:
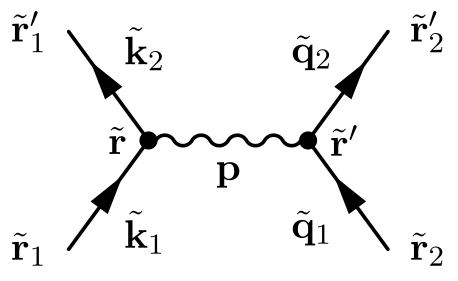$$\begin{aligned}
&= (i \hbar)^3 \sum_{s s'} \!\!\iint \dd{\tilde{\vb{r}}} \dd{\tilde{\vb{r}}'}
G_{s_1's}^0(\tilde{\vb{r}}_1', \tilde{\vb{r}}) G_{s s_1}^0(\tilde{\vb{r}}, \tilde{\vb{r}}_1) \delta_{s_1 s_1'}
W(\tilde{\vb{r}}, \tilde{\vb{r}}')
G_{s_2' s'}^0(\tilde{\vb{r}}_2', \tilde{\vb{r}}') G_{s' s_2}^0(\tilde{\vb{r}}', \tilde{\vb{r}}_2) \delta_{s_2 s_2'}
\\
&= \frac{-i \hbar^3}{(2 \pi)^{20}}
\sum_{s_1 s_2} \!\!\iint \dd{\tilde{\vb{r}}} \dd{\tilde{\vb{r}}'}
\bigg(\! \int \dd{\tilde{\vb{k}}_2} G_{s_1}^0(\tilde{\vb{k}}_2) e^{i \tilde{\vb{k}}_2 \cdot (\tilde{\vb{r}}_1' - \tilde{\vb{r}})} \!\bigg)
\bigg(\! \int \dd{\tilde{\vb{k}}_1} G_{s_1}^0(\tilde{\vb{k}}_1) e^{i \tilde{\vb{k}}_1 \cdot (\tilde{\vb{r}} - \tilde{\vb{r}}_1)} \!\bigg)
\\
&\qquad\times \bigg(\! \int \dd{\tilde{\vb{p}}} W(\tilde{\vb{p}}) e^{i \tilde{\vb{p}} \cdot (\tilde{\vb{r}}' - \tilde{\vb{r}})} \!\bigg)
\bigg(\! \int \dd{\tilde{\vb{q}}_2} G_{s_2}^0(\tilde{\vb{q}}_2) e^{i \tilde{\vb{q}}_2 \cdot (\tilde{\vb{r}}_2' - \tilde{\vb{r}}')} \!\bigg)
\bigg(\! \int \dd{\tilde{\vb{q}}_1} G_{s_2}^0(\tilde{\vb{q}}_1) e^{i \tilde{\vb{q}}_1 \cdot (\tilde{\vb{r}}' - \tilde{\vb{r}}_2)} \!\bigg)
\\
&= \frac{-i \hbar^3}{(2 \pi)^{12}}
\sum_{s_1 s_2} \!\!\iint \dd{\tilde{\vb{k}}_1} \dd{\tilde{\vb{k}}_2}
G_{s_1}^0(\tilde{\vb{k}}_2) G_{s_1}^0(\tilde{\vb{k}}_1)
\iint \dd{\tilde{\vb{q}}_1} \dd{\tilde{\vb{q}}_2}
G_{s_2}^0(\tilde{\vb{q}}_2) G_{s_2}^0(\tilde{\vb{q}}_1)
\\
&\qquad\times
e^{i \tilde{\vb{k}}_2 \cdot \tilde{\vb{r}}_1' - i \tilde{\vb{k}}_1 \cdot \tilde{\vb{r}}_1
+ i \tilde{\vb{q}}_2 \cdot \tilde{\vb{r}}_2' - i \tilde{\vb{q}}_1 \cdot \tilde{\vb{r}}_2}
\!\!\int \dd{\tilde{\vb{p}}} W(\tilde{\vb{p}})
\bigg( \frac{1}{(2 \pi)^8} \!\!\iint \dd{\tilde{\vb{r}}} \dd{\tilde{\vb{r}}'}
e^{i (\tilde{\vb{k}}_1 - \tilde{\vb{k}}_2 - \tilde{\vb{p}}) \cdot \tilde{\vb{r}}}
e^{i (\tilde{\vb{q}}_1 - \tilde{\vb{q}}_2 + \tilde{\vb{p}}) \cdot \tilde{\vb{r}}'} \bigg)
\\
&= \frac{-i \hbar^3}{(2 \pi)^{12}}
\sum_{s_1 s_2} \!\!\iint \dd{\tilde{\vb{k}}_1} \dd{\tilde{\vb{k}}_2}
G_{s_1}^0(\tilde{\vb{k}}_2) G_{s_1}^0(\tilde{\vb{k}}_1)
\iint \dd{\tilde{\vb{q}}_1} \dd{\tilde{\vb{q}}_2}
G_{s_2}^0(\tilde{\vb{q}}_2) G_{s_2}^0(\tilde{\vb{q}}_1)
\\
&\qquad\times
e^{i \tilde{\vb{k}}_2 \cdot \tilde{\vb{r}}_1' - i \tilde{\vb{k}}_1 \cdot \tilde{\vb{r}}_1
+ i \tilde{\vb{q}}_2 \cdot \tilde{\vb{r}}_2' - i \tilde{\vb{q}}_1 \cdot \tilde{\vb{r}}_2}
\!\!\int \dd{\tilde{\vb{p}}} W(\tilde{\vb{p}})
\: \delta(\tilde{\vb{k}}_1 \!-\! \tilde{\vb{k}}_2 \!-\! \tilde{\vb{p}})
\: \delta(\tilde{\vb{q}}_1 \!-\! \tilde{\vb{q}}_2 \!+\! \tilde{\vb{p}})
\\
&= \frac{-i \hbar^3}{(2 \pi)^{12}}
\sum_{s_1 s_2} \!\!\int \dd{\tilde{\vb{p}}} W(\tilde{\vb{p}})
\int \dd{\tilde{\vb{k}}_1} G_{s_1}^0(\tilde{\vb{k}}_1 \!-\! \tilde{\vb{p}}) G_{s_1}^0(\tilde{\vb{k}}_1)
\int \dd{\tilde{\vb{q}}_1} G_{s_2}^0(\tilde{\vb{q}}_1 \!+\! \tilde{\vb{p}}) G_{s_2}^0(\tilde{\vb{q}}_1)
\\
&\qquad\times
e^{i \tilde{\vb{k}}_1 \cdot (\tilde{\vb{r}}_1' - \tilde{\vb{r}}_1)}
e^{i \tilde{\vb{q}}_1 \cdot (\tilde{\vb{r}}_2' - \tilde{\vb{r}}_2)}
e^{i \tilde{\vb{p}} \cdot (\tilde{\vb{r}}_2' - \tilde{\vb{r}}_1')}
\end{aligned}$$
Conveniently, the Dirac delta functions that appear from the integrals
represent conservation of wavevector $\vb{k}$ (momentum $\hbar \vb{k}$)
and angular frequency $\omega$ (energy $\hbar \omega$).
In Fourier space, it makes more sense
to regard the incoming energies and momenta and spins as given,
and only integrate over the internal quantities.
We thus modify the Feynman diagram rules
such that we end up with the following result:
$$\begin{aligned}
\equiv \frac{-i \hbar^3}{(2 \pi)^4}
\sum_{s} \!\!\int \dd{\tilde{\vb{p}}} W(\tilde{\vb{p}})
\: G_{s_1}^0(\tilde{\vb{k}}_1 \!-\! \tilde{\vb{p}}) \: G_{s_1}^0(\tilde{\vb{k}}_1)
\: G_{s_2}^0(\tilde{\vb{q}}_1 \!+\! \tilde{\vb{p}}) \: G_{s_2}^0(\tilde{\vb{q}}_1)
\end{aligned}$$
Therefore, we say that fermion lines represent $i \hbar G_{s}^0(\vb{k}, \omega)$,
interaction lines $W(\vb{k}) / i \hbar$, etc.,
and the other interpretation rules are modified to the following:
1. Each line has a momentum $\vb{k}$ and energy $\omega$,
and each fermion line has a spin $s$;
these must all be conserved at each vertex.
2. If both ends of a *fermion* line would be at the same time,
multiply it by $e^{i \omega \eta}$,
where $\eta \to 0^+$ is a positive infinitesimal,
so e.g. $G(\tau, \tau) \to e^{i \omega \eta} G(\tau, \tau)$.
3. Integrate over all internal $(\vb{k}, \omega)$,
and sum over all internal spins $s$.
Let each $(\vb{k}, \omega)$ integral contribute a factor $1 / (2 \pi)^4$.
4. Multiply the end result by $(-1)^F$, where $F$ is the number of closed fermion loops.
5. Depending on the context, additional constant factors may be required;
sometimes they are changed on-the-fly during a calculation.
Note that if the diagram is linear (i.e. does not contain interactions),
then conservation removes all internal variables,
so no integrals would be needed.
## Imaginary time
Feynman diagrams are also useful when working with
[imaginary time](/know/concept/imaginary-time/).
In that case, the meaning of fermion lines is changed as follows,
involving the [Matsubara Green's function](/know/concept/matsubara-greens-function/):
$$\begin{aligned}
i \hbar G_{s_2 s_1}^0(\vb{r}_2, t_2; \vb{r}_1, t_1)
\:\: &\longrightarrow \:\:
-\!\hbar G_{s_2 s_1}^0(\vb{r}_2, \tau_2; \vb{r}_1, \tau_1)
= \expval{\mathcal{T} \Big\{ \hat{\Psi}_I(\vb{r}_2, \tau_2) \hat{\Psi}_I^\dagger(\vb{r}_1, \tau_1) \Big\}}
\\
i \hbar G_{s_2 s_1}(\vb{r}_2, t_2; \vb{r}_1, t_1)
\:\: &\longrightarrow \:\:
-\!\hbar G_{s_2 s_1}(\vb{r}_2, \tau_2; \vb{r}_1, \tau_1)
= \expval{\mathcal{T} \Big\{ \hat{\Psi}_H(\vb{r}_2, \tau_2) \hat{\Psi}_H^\dagger(\vb{r}_1, \tau_1) \Big\}}
\end{aligned}$$
Where the time-ordering is with respect to $\tau$.
Interaction lines are modified like so:
$$\begin{aligned}
\frac{1}{i \hbar} W_{s_2 s_1}(\vb{r}_2, t_2; \vb{r}_1, t_1)
\:\: &\longrightarrow \:\:
-\!\frac{1}{\hbar} W_{s_2 s_1}(\vb{r}_2, \tau_2; \vb{r}_1, \tau_1)
= -\frac{1}{\hbar} W(\vb{r}_2, \vb{r}_1; \tau_1) \delta(\tau_2 \!-\! \tau_1)
\end{aligned}$$
One-body $V$-vertices are usually not used,
because they are intended for real-time-dependent operators,
but in theory they would get a factor $-1/\hbar$ too.
For imaginary time, the Fourier transform is defined differently,
and a distinction must be made between
fermionic Matsubara frequencies $i \omega_n^f$ (for $G$ and $G^0$)
and bosonic Matsubara ones $i \omega_n^b$ (for $W$).
This distinction is compatible with frequency conservation,
since a sum of two fermionic frequencies is always bosonic:
$$\begin{aligned}
G_{s_2 s_1}^0(\vb{r}_2, \tau_2; \vb{r}_1, \tau_1)
&= \frac{\delta_{s_2 s_1}}{(2 \pi)^3} \int_{-\infty}^\infty \frac{1}{\hbar \beta} \sum_{n = -\infty}^\infty
G_{s_1}^0(\vb{k}, i \omega_n^f) e^{i \vb{k} \cdot (\vb{r}_2 - \vb{r}_1)} e^{- i \omega_n^f (\tau_2 - \tau_1)} \dd{\vb{k}}
\\
W_{s_2 s_1}(\vb{r}_2, \tau_2; \vb{r}_1, \tau_1)
&= \frac{1}{(2 \pi)^3} \int_{-\infty}^\infty \frac{1}{\hbar \beta} \sum_{n = -\infty}^\infty
W(\vb{k}) e^{i \vb{k} \cdot (\vb{r}_2 - \vb{r}_1)} e^{- i \omega_n^b (\tau_2 - \tau_1)} \dd{\vb{k}}
\end{aligned}$$
The interpretation in Fourier space is the same,
except that each internal integral/sum
instead gives a constant $1 / \big(\hbar \beta (2 \pi)^3\big)$,
and same-time fermion lines need a factor of $e^{i \omega_n^f \eta}$.
## References
1. H. Bruus, K. Flensberg,
*Many-body quantum theory in condensed matter physics*,
2016, Oxford.