---
title: "Quantum gate"
firstLetter: "Q"
publishDate: 2021-03-29
categories:
- Quantum information
date: 2021-03-29T21:37:57+02:00
draft: false
markup: pandoc
---
# Quantum gate
In quantum computing, **quantum gates** are the equivalent
of classical binary logic gates such as $\mathrm{NOT}$, $\mathrm{AND}$, etc.
Because of the continuous nature of qubits,
the number of possible quantum gates is uncountably infinite,
so we only consider the most important examples here.
## One-qubit gates
As an example, consider the following must general single-qubit state $\ket{\psi}$:
$$\begin{aligned}
\ket{\psi}
= \alpha \ket{0} + \beta \ket{1}
= \begin{bmatrix} \alpha \\ \beta \end{bmatrix}
\end{aligned}$$
Arguably the most famous and/or most fundamental quantum gates are the **Pauli matrices**:
$$\begin{aligned}
\boxed{
X =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
}
\qquad
\boxed{
Y =
\begin{bmatrix}
0 & -i \\
i & 0
\end{bmatrix}
}
\qquad
\boxed{
Z =
\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}
}
\end{aligned}$$
They have the following effect on $\ket{\psi}$.
Note that $X$ is equivalent to the classical $\mathrm{NOT}$ gate
(and is often given that name),
and $Z$ is sometimes called the **phase-flip gate**:
$$\begin{aligned}
X \ket{\psi}
= \begin{bmatrix} \beta \\ \alpha \end{bmatrix}
\qquad
Y \ket{\psi}
= \begin{bmatrix} -i \beta \\ i \alpha \end{bmatrix}
\qquad
Z \ket{\psi}
= \begin{bmatrix} \alpha \\ -\beta \end{bmatrix}
\end{aligned}$$
In fact, $Z$ is a specific case of the **phase shift gate** $R_\phi$,
which modifies the qubit's phase without changing its amplitudes.
For an angle $\phi$, it is given by:
$$\begin{aligned}
\boxed{
R_\phi =
\begin{bmatrix}
1 & 0 \\
0 & e^{i \phi}
\end{bmatrix}
}
\end{aligned}$$
For $\phi = \pi$, we recover the Pauli-$Z$ gate.
In general, the action of $R_\phi$ is as follows:
$$\begin{aligned}
R_\phi \ket{\psi}
= \begin{bmatrix} \alpha \\ e^{i \phi} \beta \end{bmatrix}
\end{aligned}$$
Two common special cases of $R_\phi$
are $\phi = \pi/2$ and $\phi = \pi/4$,
respectively called $S$ and $T$:
$$\begin{aligned}
\boxed{
S = R_{\pi/2} =
\begin{bmatrix}
1 & 0 \\
0 & i
\end{bmatrix}
}
\qquad \quad
\boxed{
T = R_{\pi/4} =
\frac{1}{\sqrt{2}}
\begin{bmatrix}
\sqrt{2} & 0 \\
0 & 1 + i
\end{bmatrix}
}
\end{aligned}$$
Finally, we have the **Hadamard gate** $H$,
which is defined as follows:
$$\begin{aligned}
\boxed{
H = \frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
}
\end{aligned}$$
Its action consists of rotating the qubit
by $\pi$ around the axis $(X + Z) / \sqrt{2}$ of the Bloch sphere:
$$\begin{aligned}
H \ket{\psi}
= \frac{1}{\sqrt{2}} \begin{bmatrix} \alpha + \beta \\ \alpha - \beta \end{bmatrix}
\end{aligned}$$
Notably, it maps the eigenstates of $X$ and $Z$ to each other,
and is its own inverse (i.e. unitary):
$$\begin{aligned}
H \ket{0} = \ket{+}
\qquad
H \ket{1} = \ket{-}
\qquad
H \ket{+} = \ket{0}
\qquad
H \ket{-} = \ket{1}
\end{aligned}$$
The **Clifford gates** are a set including $X$, $Y$, $Z$, $H$ and $S$,
or more generally any gates that rotate
by multiples of $\pi/2$ around the Bloch sphere.
This set is **not universal**, meaning that if we start from $\ket{0}$,
we can only reach $\ket{0}$, $\ket{1}$, $\ket{+}$, $\ket{-}$, $\ket{+i}$ $\ket{-i}$ using these gates.
If we add *any* non-Clifford gate, for example $T$,
then we can reach any point on the Bloch sphere,
which means that the set is **universal**.
However, there is a problem: a qubit has an uncountable infinity of states,
but a quantum circuit consists of a countably infinite sequence of gates, at most.
Therefore, technically, we can never reach the whole Bloch sphere,
but we *can* come up with circuits that approximate a target state to some degree $\varepsilon$.
This is the definition of universality:
any state can be approximated.
## Two-qubit gates
As an example, let us consider
the following two pure one-qubit states $\ket{\psi_1}$ and $\ket{\psi_2}$:
$$\begin{aligned}
\ket{\psi_1}
= \alpha_1 \ket{0} + \beta_1 \ket{1}
= \begin{bmatrix} \alpha_1 \\ \beta_1 \end{bmatrix}
\qquad \quad
\ket{\psi_2}
= \alpha_2 \ket{0} + \beta_2 \ket{1}
= \begin{bmatrix} \alpha_2 \\ \beta_2 \end{bmatrix}
\end{aligned}$$
The composite state of both qubits, assuming they are pure,
is then their tensor product $\otimes$:
$$\begin{aligned}
\ket{\psi_1 \psi_2}
= \ket{\psi_1} \otimes \ket{\psi_2}
&= \alpha_1 \alpha_2 \ket{00} + \alpha_1 \beta_2 \ket{01} + \beta_1 \alpha_2 \ket{10} + \beta_1 \beta_2 \ket{11}
\\
&= c_{00} \ket{00} + c_{01} \ket{01} + c_{10} \ket{10} + c_{11} \ket{11}
\end{aligned}$$
Note that a two-qubit system may be [entangled](/know/concept/quantum-entanglement/),
in which case the coefficients $c_{00}$ etc. cannot be written as products,
i.e. $\ket{\psi_2}$ cannot be expressed separately from $\ket{\psi_1}$, and vice versa.
In other words, the general action of a two-qubit quantum gate
can be expressed in the basis of $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$,
but not always in the basis of $\ket{0}_1$, $\ket{1}_1$, $\ket{0}_2$ and $\ket{1}_2$.
With that said, the first two-qubit gate is $\mathrm{SWAP}$,
which simply swaps $\ket{\psi_1}$ and $\ket{\psi_2}$:
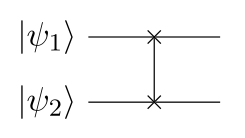 $$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$.
Note that $\mathrm{SWAP}$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{10} \ket{01} + c_{01} \ket{10} + c_{11} \ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $\mathrm{CNOT}$,
which "flips" (applies $X$ to) $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
$$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$.
Note that $\mathrm{SWAP}$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{10} \ket{01} + c_{01} \ket{10} + c_{11} \ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $\mathrm{CNOT}$,
which "flips" (applies $X$ to) $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
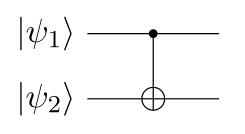 $$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $c_{10}$ and $c_{11}$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + c_{11} \ket{10} + c_{10} \ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $U$,
we can define a two-qubit **controlled U gate** $\mathrm{CU}$,
which applies $U$ to $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
$$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $c_{10}$ and $c_{11}$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + c_{11} \ket{10} + c_{10} \ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $U$,
we can define a two-qubit **controlled U gate** $\mathrm{CU}$,
which applies $U$ to $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
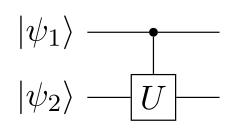 $$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $U$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $n$ to $n$ qubits can be approximated using only these gates.
A minimal universal set is $\{\mathrm{CNOT}, T, S\}$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
$$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $U$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $n$ to $n$ qubits can be approximated using only these gates.
A minimal universal set is $\{\mathrm{CNOT}, T, S\}$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
 $$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$.
Note that $\mathrm{SWAP}$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{10} \ket{01} + c_{01} \ket{10} + c_{11} \ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $\mathrm{CNOT}$,
which "flips" (applies $X$ to) $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
$$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$.
Note that $\mathrm{SWAP}$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{10} \ket{01} + c_{01} \ket{10} + c_{11} \ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $\mathrm{CNOT}$,
which "flips" (applies $X$ to) $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
 $$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $c_{10}$ and $c_{11}$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + c_{11} \ket{10} + c_{10} \ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $U$,
we can define a two-qubit **controlled U gate** $\mathrm{CU}$,
which applies $U$ to $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
$$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $c_{10}$ and $c_{11}$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + c_{11} \ket{10} + c_{10} \ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $U$,
we can define a two-qubit **controlled U gate** $\mathrm{CU}$,
which applies $U$ to $\ket{\psi_2}$ if $\ket{\psi_1}$ is true:
 $$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $U$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $n$ to $n$ qubits can be approximated using only these gates.
A minimal universal set is $\{\mathrm{CNOT}, T, S\}$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
$$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $U$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \ket{\psi_1 \psi_2}
&= c_{00} \ket{00} + c_{01} \ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $n$ to $n$ qubits can be approximated using only these gates.
A minimal universal set is $\{\mathrm{CNOT}, T, S\}$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.