---
title: "Random phase approximation"
firstLetter: "R"
publishDate: 2021-12-01
categories:
- Physics
- Quantum mechanics
date: 2021-11-15T21:01:34+01:00
draft: false
markup: pandoc
---
# Random phase approximation
Recall that the [self-energy](/know/concept/self-energy/) $\Sigma$
is defined as a sum of [Feynman diagrams](/know/concept/feynman-diagram/),
which each have an order $n$ equal to the number of interaction lines.
We consider the self-energy in the context of [jellium](/know/concept/jellium/),
so the interaction lines $W$ represent Coulomb repulsion,
and we use [imaginary time](/know/concept/imaginary-time/).
Let us non-dimensionalize the Feynman diagrams in the self-energy,
by measuring momenta in units of $\hbar k_F$,
and energies in $\epsilon_F = \hbar^2 k_F^2 / (2 m)$.
Each internal variable then gives a factor $k_F^5$,
where $k_F^3$ comes from the 3D momentum integral,
and $k_F^2$ from the energy $1 / \beta$:
$$\begin{aligned}
\frac{1}{(2 \pi)^3} \int_{-\infty}^\infty \frac{1}{\hbar \beta} \sum_{n = -\infty}^\infty \cdots \:\dd{\vb{k}}
\:\:\sim\:\:
k_F^5
\end{aligned}$$
Meanwhile, every line gives a factor $1 / k_F^2$.
The [Matsubara Green's function](/know/concept/matsubara-greens-function/) $G^0$
for a system with continuous translational symmetry
is found from [equation-of-motion theory](/know/concept/equation-of-motion-theory/):
$$\begin{aligned}
W(\vb{k}) = \frac{e^2}{\varepsilon_0 |\vb{k}|^2}
\:\:\sim\:\:
\frac{1}{k_F^2}
\qquad \qquad
G_s^0(\vb{k}, i \omega_n^F)
= \frac{1}{i \hbar \omega_n^F - \varepsilon_\vb{k}}
\:\:\sim\:\:
\frac{1}{k_F^2}
\end{aligned}$$
An $n$th-order diagram in $\Sigma$ contains $n$ interaction lines,
$2n\!-\!1$ fermion lines, and $n$ integrals,
so in total it evolves as $1 / k_F^{n-2}$.
In jellium, we know that the electron density is proportional to $k_F^3$,
so for high densities we can rest assured that higher-order terms in $\Sigma$
converge to zero faster than lower-order terms.
However, at a given order $n$, not all diagrams are equally important.
In a given diagram, due to momentum conservation,
some interaction lines carry the same momentum variable.
Because $W(\vb{k}) \propto 1 / |\vb{k}|^2$,
small $\vb{k}$ make a large contribution,
and the more interaction lines depend on the same $\vb{k}$,
the larger the contribution becomes.
In other words, each diagram is dominated by contributions
from the momentum carried by the largest number of interactions.
At order $n$, there is one diagram
where all $n$ interactions carry the same momentum,
and this one dominates all others at this order.
The **random phase approximation** consists of removing most diagrams
from the defintion of the full self-energy $\Sigma$,
leaving only the single most divergent one at each order $n$,
i.e. the ones where all $n$ interaction lines
carry the same momentum and energy:
 Where we have defined the **screened interaction** $W^\mathrm{RPA}$,
denoted by a double wavy line:
Where we have defined the **screened interaction** $W^\mathrm{RPA}$,
denoted by a double wavy line:
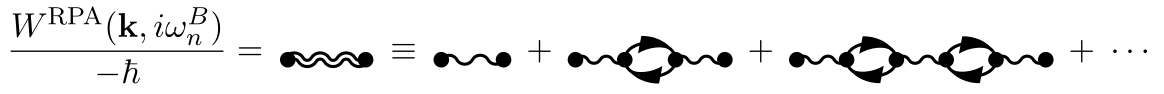 Rearranging the above sequence of diagrams quickly leads to the following
[Dyson equation](/know/concept/dyson-equation/):
Rearranging the above sequence of diagrams quickly leads to the following
[Dyson equation](/know/concept/dyson-equation/):
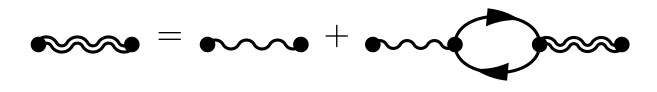 In Fourier space, this equation's linear shape
means it is algebraic, so we can write it out:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}
= W + W \Pi_0 W^\mathrm{RPA}
}
\end{aligned}$$
Where we have defined the **pair-bubble** $\Pi_0$ as follows,
with an internal wavevector $\vb{q}$, fermionic frequency $i \omega_m^F$, and spin $s$.
Abbreviating $\tilde{\vb{k}} \equiv (\vb{k}, i \omega_n^B)$
and $\tilde{\vb{q}} \equiv (\vb{q}, i \omega_n^F)$:
In Fourier space, this equation's linear shape
means it is algebraic, so we can write it out:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}
= W + W \Pi_0 W^\mathrm{RPA}
}
\end{aligned}$$
Where we have defined the **pair-bubble** $\Pi_0$ as follows,
with an internal wavevector $\vb{q}$, fermionic frequency $i \omega_m^F$, and spin $s$.
Abbreviating $\tilde{\vb{k}} \equiv (\vb{k}, i \omega_n^B)$
and $\tilde{\vb{q}} \equiv (\vb{q}, i \omega_n^F)$:
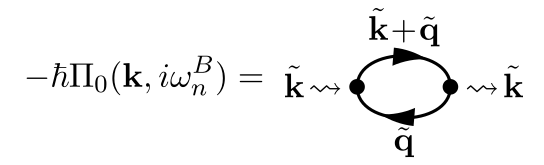 We isolate the Dyson equation for $W^\mathrm{RPA}$,
which reveals its physical interpretation as a *screened* interaction:
the "raw" interaction $W \!=\! e^2 / (\varepsilon_0 |\vb{k}|^2)$
is weakened by a term containing $\Pi_0$:
$$\begin{aligned}
W^\mathrm{RPA}(\vb{k}, i \omega_n^B)
= \frac{W(\vb{k})}{1 - W(\vb{k}) \: \Pi_0(\vb{k}, i \omega_n^B)}
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, i \omega_n^B)}
\end{aligned}$$
Let us evaluate the pair-bubble $\Pi_0$ more concretely.
The Feynman diagram translates to:
$$\begin{aligned}
-\hbar \Pi_0(\vb{k}, i \omega_n^B)
&= - \sum_{s} \frac{1}{(2 \pi)^3} \int \frac{1}{\hbar \beta} \sum_{m = -\infty}^\infty
\hbar G_s(\vb{k} \!+\! \vb{q}, i \omega_n^B \!+\! i \omega_m^F) \: \hbar G_s(\vb{q}, i \omega_m^F) \dd{\vb{q}}
\\
&= - \frac{2 \hbar}{(2 \pi)^3} \int \frac{1}{\beta} \sum_{m = -\infty}^\infty
\frac{1}{i \hbar \omega_n^B + i \hbar \omega_m^F - \varepsilon_{\vb{k}+\vb{q}}} \: \frac{1}{i \hbar \omega_m^F - \varepsilon_{\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Here we recognize a [Matsubara sum](/know/concept/matsubara-sum/),
and rewrite accordingly.
Note that the residues of $n_F$ are $1 / (\hbar \beta)$
when it is a function of frequency,
and $1 / \beta$ when it is a function of energy, so:
$$\begin{aligned}
\Pi_0(\vb{k}, i \omega_n^B)
&= \frac{2}{(2 \pi)^3} \int
\frac{n_F(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B)}{(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B) - \varepsilon_{\vb{q}}}
+ \frac{n_F(\varepsilon_{\vb{q}})}{i \hbar \omega_n^B + (\varepsilon_{\vb{q}}) - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\\
&= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{i \hbar \omega_n^B + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Where we have used that $n_F(\varepsilon \!+\! i \hbar \omega_n^B) = n_F(\varepsilon)$.
Analogously to extracting the retarded Green's function $G^R(\omega)$
from the Matsubara Green's function $G^0(i \omega_n^F)$,
we replace $i \omega_n^F \to \omega \!+\! i \eta$,
where $\eta \to 0^+$ is a positive infinitesimal,
yielding the retarded pair-bubble $\Pi_0^R$:
$$\begin{aligned}
\boxed{
\Pi_0^R(\vb{k}, \omega)
= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{\hbar (\omega + i \eta) + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
}
\end{aligned}$$
This is as far as we can go before making simplifying assumptions.
Therefore, we leave it at:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}(\vb{k}, \omega)
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, \omega)}
}
\end{aligned}$$
## References
1. H. Bruus, K. Flensberg,
*Many-body quantum theory in condensed matter physics*,
2016, Oxford.
We isolate the Dyson equation for $W^\mathrm{RPA}$,
which reveals its physical interpretation as a *screened* interaction:
the "raw" interaction $W \!=\! e^2 / (\varepsilon_0 |\vb{k}|^2)$
is weakened by a term containing $\Pi_0$:
$$\begin{aligned}
W^\mathrm{RPA}(\vb{k}, i \omega_n^B)
= \frac{W(\vb{k})}{1 - W(\vb{k}) \: \Pi_0(\vb{k}, i \omega_n^B)}
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, i \omega_n^B)}
\end{aligned}$$
Let us evaluate the pair-bubble $\Pi_0$ more concretely.
The Feynman diagram translates to:
$$\begin{aligned}
-\hbar \Pi_0(\vb{k}, i \omega_n^B)
&= - \sum_{s} \frac{1}{(2 \pi)^3} \int \frac{1}{\hbar \beta} \sum_{m = -\infty}^\infty
\hbar G_s(\vb{k} \!+\! \vb{q}, i \omega_n^B \!+\! i \omega_m^F) \: \hbar G_s(\vb{q}, i \omega_m^F) \dd{\vb{q}}
\\
&= - \frac{2 \hbar}{(2 \pi)^3} \int \frac{1}{\beta} \sum_{m = -\infty}^\infty
\frac{1}{i \hbar \omega_n^B + i \hbar \omega_m^F - \varepsilon_{\vb{k}+\vb{q}}} \: \frac{1}{i \hbar \omega_m^F - \varepsilon_{\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Here we recognize a [Matsubara sum](/know/concept/matsubara-sum/),
and rewrite accordingly.
Note that the residues of $n_F$ are $1 / (\hbar \beta)$
when it is a function of frequency,
and $1 / \beta$ when it is a function of energy, so:
$$\begin{aligned}
\Pi_0(\vb{k}, i \omega_n^B)
&= \frac{2}{(2 \pi)^3} \int
\frac{n_F(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B)}{(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B) - \varepsilon_{\vb{q}}}
+ \frac{n_F(\varepsilon_{\vb{q}})}{i \hbar \omega_n^B + (\varepsilon_{\vb{q}}) - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\\
&= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{i \hbar \omega_n^B + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Where we have used that $n_F(\varepsilon \!+\! i \hbar \omega_n^B) = n_F(\varepsilon)$.
Analogously to extracting the retarded Green's function $G^R(\omega)$
from the Matsubara Green's function $G^0(i \omega_n^F)$,
we replace $i \omega_n^F \to \omega \!+\! i \eta$,
where $\eta \to 0^+$ is a positive infinitesimal,
yielding the retarded pair-bubble $\Pi_0^R$:
$$\begin{aligned}
\boxed{
\Pi_0^R(\vb{k}, \omega)
= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{\hbar (\omega + i \eta) + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
}
\end{aligned}$$
This is as far as we can go before making simplifying assumptions.
Therefore, we leave it at:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}(\vb{k}, \omega)
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, \omega)}
}
\end{aligned}$$
## References
1. H. Bruus, K. Flensberg,
*Many-body quantum theory in condensed matter physics*,
2016, Oxford.
 Where we have defined the **screened interaction** $W^\mathrm{RPA}$,
denoted by a double wavy line:
Where we have defined the **screened interaction** $W^\mathrm{RPA}$,
denoted by a double wavy line:
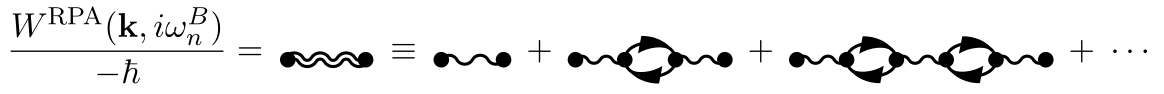 Rearranging the above sequence of diagrams quickly leads to the following
[Dyson equation](/know/concept/dyson-equation/):
Rearranging the above sequence of diagrams quickly leads to the following
[Dyson equation](/know/concept/dyson-equation/):
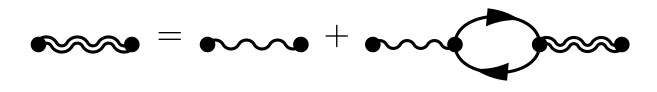 In Fourier space, this equation's linear shape
means it is algebraic, so we can write it out:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}
= W + W \Pi_0 W^\mathrm{RPA}
}
\end{aligned}$$
Where we have defined the **pair-bubble** $\Pi_0$ as follows,
with an internal wavevector $\vb{q}$, fermionic frequency $i \omega_m^F$, and spin $s$.
Abbreviating $\tilde{\vb{k}} \equiv (\vb{k}, i \omega_n^B)$
and $\tilde{\vb{q}} \equiv (\vb{q}, i \omega_n^F)$:
In Fourier space, this equation's linear shape
means it is algebraic, so we can write it out:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}
= W + W \Pi_0 W^\mathrm{RPA}
}
\end{aligned}$$
Where we have defined the **pair-bubble** $\Pi_0$ as follows,
with an internal wavevector $\vb{q}$, fermionic frequency $i \omega_m^F$, and spin $s$.
Abbreviating $\tilde{\vb{k}} \equiv (\vb{k}, i \omega_n^B)$
and $\tilde{\vb{q}} \equiv (\vb{q}, i \omega_n^F)$:
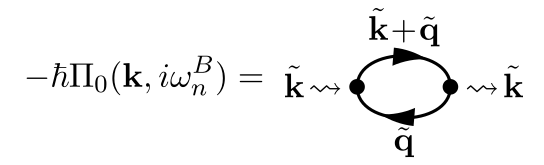 We isolate the Dyson equation for $W^\mathrm{RPA}$,
which reveals its physical interpretation as a *screened* interaction:
the "raw" interaction $W \!=\! e^2 / (\varepsilon_0 |\vb{k}|^2)$
is weakened by a term containing $\Pi_0$:
$$\begin{aligned}
W^\mathrm{RPA}(\vb{k}, i \omega_n^B)
= \frac{W(\vb{k})}{1 - W(\vb{k}) \: \Pi_0(\vb{k}, i \omega_n^B)}
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, i \omega_n^B)}
\end{aligned}$$
Let us evaluate the pair-bubble $\Pi_0$ more concretely.
The Feynman diagram translates to:
$$\begin{aligned}
-\hbar \Pi_0(\vb{k}, i \omega_n^B)
&= - \sum_{s} \frac{1}{(2 \pi)^3} \int \frac{1}{\hbar \beta} \sum_{m = -\infty}^\infty
\hbar G_s(\vb{k} \!+\! \vb{q}, i \omega_n^B \!+\! i \omega_m^F) \: \hbar G_s(\vb{q}, i \omega_m^F) \dd{\vb{q}}
\\
&= - \frac{2 \hbar}{(2 \pi)^3} \int \frac{1}{\beta} \sum_{m = -\infty}^\infty
\frac{1}{i \hbar \omega_n^B + i \hbar \omega_m^F - \varepsilon_{\vb{k}+\vb{q}}} \: \frac{1}{i \hbar \omega_m^F - \varepsilon_{\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Here we recognize a [Matsubara sum](/know/concept/matsubara-sum/),
and rewrite accordingly.
Note that the residues of $n_F$ are $1 / (\hbar \beta)$
when it is a function of frequency,
and $1 / \beta$ when it is a function of energy, so:
$$\begin{aligned}
\Pi_0(\vb{k}, i \omega_n^B)
&= \frac{2}{(2 \pi)^3} \int
\frac{n_F(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B)}{(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B) - \varepsilon_{\vb{q}}}
+ \frac{n_F(\varepsilon_{\vb{q}})}{i \hbar \omega_n^B + (\varepsilon_{\vb{q}}) - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\\
&= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{i \hbar \omega_n^B + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Where we have used that $n_F(\varepsilon \!+\! i \hbar \omega_n^B) = n_F(\varepsilon)$.
Analogously to extracting the retarded Green's function $G^R(\omega)$
from the Matsubara Green's function $G^0(i \omega_n^F)$,
we replace $i \omega_n^F \to \omega \!+\! i \eta$,
where $\eta \to 0^+$ is a positive infinitesimal,
yielding the retarded pair-bubble $\Pi_0^R$:
$$\begin{aligned}
\boxed{
\Pi_0^R(\vb{k}, \omega)
= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{\hbar (\omega + i \eta) + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
}
\end{aligned}$$
This is as far as we can go before making simplifying assumptions.
Therefore, we leave it at:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}(\vb{k}, \omega)
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, \omega)}
}
\end{aligned}$$
## References
1. H. Bruus, K. Flensberg,
*Many-body quantum theory in condensed matter physics*,
2016, Oxford.
We isolate the Dyson equation for $W^\mathrm{RPA}$,
which reveals its physical interpretation as a *screened* interaction:
the "raw" interaction $W \!=\! e^2 / (\varepsilon_0 |\vb{k}|^2)$
is weakened by a term containing $\Pi_0$:
$$\begin{aligned}
W^\mathrm{RPA}(\vb{k}, i \omega_n^B)
= \frac{W(\vb{k})}{1 - W(\vb{k}) \: \Pi_0(\vb{k}, i \omega_n^B)}
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, i \omega_n^B)}
\end{aligned}$$
Let us evaluate the pair-bubble $\Pi_0$ more concretely.
The Feynman diagram translates to:
$$\begin{aligned}
-\hbar \Pi_0(\vb{k}, i \omega_n^B)
&= - \sum_{s} \frac{1}{(2 \pi)^3} \int \frac{1}{\hbar \beta} \sum_{m = -\infty}^\infty
\hbar G_s(\vb{k} \!+\! \vb{q}, i \omega_n^B \!+\! i \omega_m^F) \: \hbar G_s(\vb{q}, i \omega_m^F) \dd{\vb{q}}
\\
&= - \frac{2 \hbar}{(2 \pi)^3} \int \frac{1}{\beta} \sum_{m = -\infty}^\infty
\frac{1}{i \hbar \omega_n^B + i \hbar \omega_m^F - \varepsilon_{\vb{k}+\vb{q}}} \: \frac{1}{i \hbar \omega_m^F - \varepsilon_{\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Here we recognize a [Matsubara sum](/know/concept/matsubara-sum/),
and rewrite accordingly.
Note that the residues of $n_F$ are $1 / (\hbar \beta)$
when it is a function of frequency,
and $1 / \beta$ when it is a function of energy, so:
$$\begin{aligned}
\Pi_0(\vb{k}, i \omega_n^B)
&= \frac{2}{(2 \pi)^3} \int
\frac{n_F(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B)}{(\varepsilon_{\vb{k}+\vb{q}} - i \hbar \omega_n^B) - \varepsilon_{\vb{q}}}
+ \frac{n_F(\varepsilon_{\vb{q}})}{i \hbar \omega_n^B + (\varepsilon_{\vb{q}}) - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\\
&= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{i \hbar \omega_n^B + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
\end{aligned}$$
Where we have used that $n_F(\varepsilon \!+\! i \hbar \omega_n^B) = n_F(\varepsilon)$.
Analogously to extracting the retarded Green's function $G^R(\omega)$
from the Matsubara Green's function $G^0(i \omega_n^F)$,
we replace $i \omega_n^F \to \omega \!+\! i \eta$,
where $\eta \to 0^+$ is a positive infinitesimal,
yielding the retarded pair-bubble $\Pi_0^R$:
$$\begin{aligned}
\boxed{
\Pi_0^R(\vb{k}, \omega)
= \frac{2}{(2 \pi)^3} \int \frac{n_F(\varepsilon_{\vb{q}}) - n_F(\varepsilon_{\vb{k}+\vb{q}})}
{\hbar (\omega + i \eta) + \varepsilon_{\vb{q}} - \varepsilon_{\vb{k}+\vb{q}}} \dd{\vb{q}}
}
\end{aligned}$$
This is as far as we can go before making simplifying assumptions.
Therefore, we leave it at:
$$\begin{aligned}
\boxed{
W^\mathrm{RPA}(\vb{k}, \omega)
= \frac{e^2}{\varepsilon_0 |\vb{k}|^2 - e^2 \Pi_0(\vb{k}, \omega)}
}
\end{aligned}$$
## References
1. H. Bruus, K. Flensberg,
*Many-body quantum theory in condensed matter physics*,
2016, Oxford.