---
title: "Repetition code"
firstLetter: "R"
publishDate: 2021-05-07
categories:
- Quantum information
date: 2021-05-07T15:10:43+02:00
draft: false
markup: pandoc
---
# Repetition code
A **repetition code** is a simple approach to error correction:
to protect a bit $x$, make two copies:
$$\begin{aligned}
0 \to 000
\qquad \quad
1 \to 111
\end{aligned}$$
If a single-bit error occurs, e.g. $000 \to 100$,
a majority vote resets the minority bit.
Clearly, this does not protect against multi-bit errors,
but that is usually not necessary.
In quantum computing, where error correction is much more important,
repetition codes can also be used,
albeit with some complications,
as discussed below.
## Bit flip code
Suppose that we want to detect errors in
the following arbitrary qubit state $\ket{\psi}$:
$$\begin{aligned}
\ket{\psi}
= \alpha \ket{0} + \beta \ket{1}
\end{aligned}$$
For now, let us limit ourselves to detecting **bit flips**,
where $\alpha$ and $\beta$ get switched:
$$\begin{aligned}
\alpha \ket{0} + \beta \ket{1}
\quad \to \boxed{\mathrm{Error}} \to \quad
\beta \ket{0} \!+\! \alpha \ket{1}
\end{aligned}$$
One way to defend against this is
the quantum version of a classical repetition code:
$$\begin{aligned}
\ket{\psi}
\quad \to \boxed{\mathrm{Encoder}} \to \quad
\ket*{\overline{\psi}}
= \alpha \ket{000} + \beta \ket{111}
\end{aligned}$$
In other words, a *logical* $\ket{0}$ (written $\ket*{\overline{0}}$)
is represented by 3 *physical* qubits, and vice versa:
$$\begin{aligned}
\boxed{
\ket{0}
\to
\ket*{\overline{0}}
= \ket{000}
\qquad \quad
\ket{1}
\to
\ket*{\overline{1}}
= \ket{111}
}
\end{aligned}$$
Such a transformation is easy to achieve with the following sequence
of [quantum gates](/know/concept/quantum-gate/):
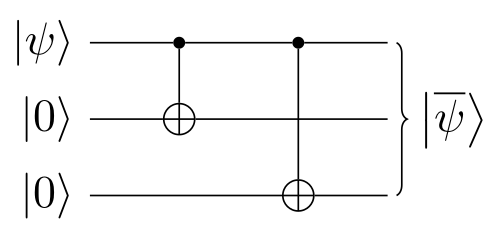 So, a little while after encoding the state $\ket{\psi}$ like that,
a bit flip occurs on the 2nd qubit:
$$\begin{aligned}
\ket*{\overline{\psi}}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{010} + \beta \ket{101}
\end{aligned}$$
But now there is a problem: how do we detect this error?
We could measure the state, but that would make it collapse,
which is probably not what we want.
The trick is to use operators called **stabilizers**,
in this case for example $ZZI = Z_1 \otimes Z_2 \otimes I_3$,
where $I$ is identity and $Z$ is the Pauli-$Z$ gate.
The 3-qubit basis states are its eigenvectors:
$$\begin{alignedat}{2}
ZZI \ket{000}
&= + \ket{000}
\qquad
ZZI \ket{001}
&&= + \ket{001}
\\
ZZI \ket{010}
&= - \ket{010}
\qquad
ZZI \ket{011}
&&= - \ket{011}
\\
ZZI \ket{100}
&= - \ket{100}
\qquad
ZZI \ket{101}
&&= - \ket{101}
\\
ZZI \ket{110}
&= + \ket{110}
\qquad
ZZI \ket{111}
&&= + \ket{111}
\end{alignedat}$$
We could measure $ZZI$ for $\ket*{\overline{\psi}}$,
and if the eigenvalue is $-1$,
we know that a bit flip has occurred,
whereas if the eigenvalue is $+1$,
there is *maybe* no error ($\ket{001}$ and $\ket{110}$ are false negatives).
These false negatives are fixed by including another stabilizer $IZZ$,
with these eigenvectors:
$$\begin{alignedat}{2}
IZZ \ket{000}
&= + \ket{000}
\qquad
IZZ \ket{001}
&&= - \ket{001}
\\
IZZ \ket{010}
&= - \ket{010}
\qquad
IZZ \ket{011}
&&= + \ket{011}
\\
IZZ \ket{100}
&= + \ket{100}
\qquad
IZZ \ket{101}
&&= - \ket{101}
\\
IZZ \ket{110}
&= - \ket{110}
\qquad
IZZ \ket{111}
&&= + \ket{111}
\end{alignedat}$$
In which case $\ket{100}$ and $\ket{011}$ are false negatives.
In other words, $IZZ$ cannot detect if the 1st qubit was flipped,
while $ZZI$ cannot protect the 3rd qubit.
But by using both, we know exactly which qubit was flipped
thanks to the eigenvalues:
So, a little while after encoding the state $\ket{\psi}$ like that,
a bit flip occurs on the 2nd qubit:
$$\begin{aligned}
\ket*{\overline{\psi}}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{010} + \beta \ket{101}
\end{aligned}$$
But now there is a problem: how do we detect this error?
We could measure the state, but that would make it collapse,
which is probably not what we want.
The trick is to use operators called **stabilizers**,
in this case for example $ZZI = Z_1 \otimes Z_2 \otimes I_3$,
where $I$ is identity and $Z$ is the Pauli-$Z$ gate.
The 3-qubit basis states are its eigenvectors:
$$\begin{alignedat}{2}
ZZI \ket{000}
&= + \ket{000}
\qquad
ZZI \ket{001}
&&= + \ket{001}
\\
ZZI \ket{010}
&= - \ket{010}
\qquad
ZZI \ket{011}
&&= - \ket{011}
\\
ZZI \ket{100}
&= - \ket{100}
\qquad
ZZI \ket{101}
&&= - \ket{101}
\\
ZZI \ket{110}
&= + \ket{110}
\qquad
ZZI \ket{111}
&&= + \ket{111}
\end{alignedat}$$
We could measure $ZZI$ for $\ket*{\overline{\psi}}$,
and if the eigenvalue is $-1$,
we know that a bit flip has occurred,
whereas if the eigenvalue is $+1$,
there is *maybe* no error ($\ket{001}$ and $\ket{110}$ are false negatives).
These false negatives are fixed by including another stabilizer $IZZ$,
with these eigenvectors:
$$\begin{alignedat}{2}
IZZ \ket{000}
&= + \ket{000}
\qquad
IZZ \ket{001}
&&= - \ket{001}
\\
IZZ \ket{010}
&= - \ket{010}
\qquad
IZZ \ket{011}
&&= + \ket{011}
\\
IZZ \ket{100}
&= + \ket{100}
\qquad
IZZ \ket{101}
&&= - \ket{101}
\\
IZZ \ket{110}
&= - \ket{110}
\qquad
IZZ \ket{111}
&&= + \ket{111}
\end{alignedat}$$
In which case $\ket{100}$ and $\ket{011}$ are false negatives.
In other words, $IZZ$ cannot detect if the 1st qubit was flipped,
while $ZZI$ cannot protect the 3rd qubit.
But by using both, we know exactly which qubit was flipped
thanks to the eigenvalues:
| Error |
$ZZI$ |
$IZZ$ |
| $I$ |
$+1$ |
$+1$ |
| $X_1$ |
$-1$ |
$+1$ |
| $X_2$ |
$-1$ |
$-1$ |
| $X_1$ |
$+1$ |
$-1$ |
Where e.g. $X_3$ denotes that the 3rd qubit was flipped.
The measurement outcomes on the last three rows are called **error syndromes**,
and are obtained by a **syndrome measurement**.
Fortunately, we can measure $ZZI$ and $IZZ$
without affecting $\ket*{\overline{\psi}}$ itself,
by applying $\mathrm{CNOT}$s to some ancillary qubits
and then measuring those:
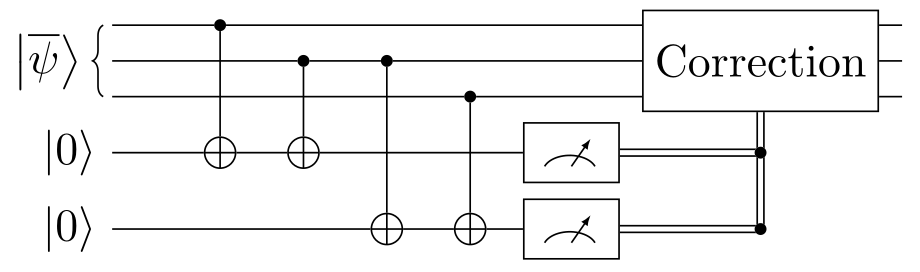 The two measurements, respectively representing $ZZI$ and $IZZ$,
yield $\ket{1}$ if a bit flip definitely occurred,
and $\ket{0}$ otherwise.
There is no entanglement,
so the input is untouched.
## Phase flip code
The above system protects us against all single-qubit bit flips.
Unfortunately, that is not enough:
qubits can also experience a **phase flip**:
$$\begin{aligned}
\alpha \ket{0} + \beta \ket{1}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{0} - \beta \ket{1}
\end{aligned}$$
How to detect that?
If we want to protect against phase flips *instead of* bit flips,
we can simply do the same as before,
but along the $X$-axis intead of the $Z$-axis:
$$\begin{aligned}
\boxed{
\ket{0}
\to
\ket*{\overline{0}}
= \ket{+\!+\!+}
\qquad \quad
\ket{1}
\to
\ket*{\overline{1}}
= \ket{-\!-\!-}
}
\end{aligned}$$
Such that an arbitrary state $\ket{\psi}$ is encoded as follows,
by the circuit shown below:
$$\begin{aligned}
\ket{\psi}
\quad \to \boxed{\mathrm{Encoder}} \to \quad
\ket*{\overline{\psi}}
= \alpha \ket{+\!+\!+} + \beta \ket{-\!-\!-}
\end{aligned}$$
The two measurements, respectively representing $ZZI$ and $IZZ$,
yield $\ket{1}$ if a bit flip definitely occurred,
and $\ket{0}$ otherwise.
There is no entanglement,
so the input is untouched.
## Phase flip code
The above system protects us against all single-qubit bit flips.
Unfortunately, that is not enough:
qubits can also experience a **phase flip**:
$$\begin{aligned}
\alpha \ket{0} + \beta \ket{1}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{0} - \beta \ket{1}
\end{aligned}$$
How to detect that?
If we want to protect against phase flips *instead of* bit flips,
we can simply do the same as before,
but along the $X$-axis intead of the $Z$-axis:
$$\begin{aligned}
\boxed{
\ket{0}
\to
\ket*{\overline{0}}
= \ket{+\!+\!+}
\qquad \quad
\ket{1}
\to
\ket*{\overline{1}}
= \ket{-\!-\!-}
}
\end{aligned}$$
Such that an arbitrary state $\ket{\psi}$ is encoded as follows,
by the circuit shown below:
$$\begin{aligned}
\ket{\psi}
\quad \to \boxed{\mathrm{Encoder}} \to \quad
\ket*{\overline{\psi}}
= \alpha \ket{+\!+\!+} + \beta \ket{-\!-\!-}
\end{aligned}$$
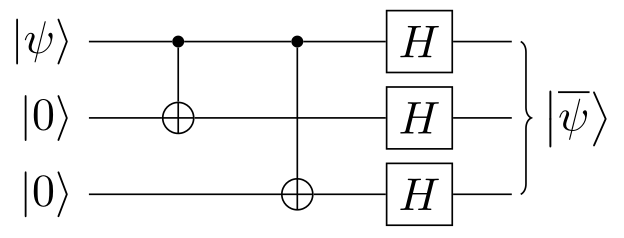 A phase flip along the $Z$-axis
corresponds to a bit flip along the $X$-axis $\ket{+} \to \ket{-}$.
In this case, the stabilizers are $XXI$ and $IXX$,
and the error detection circuit is as follows:
A phase flip along the $Z$-axis
corresponds to a bit flip along the $X$-axis $\ket{+} \to \ket{-}$.
In this case, the stabilizers are $XXI$ and $IXX$,
and the error detection circuit is as follows:
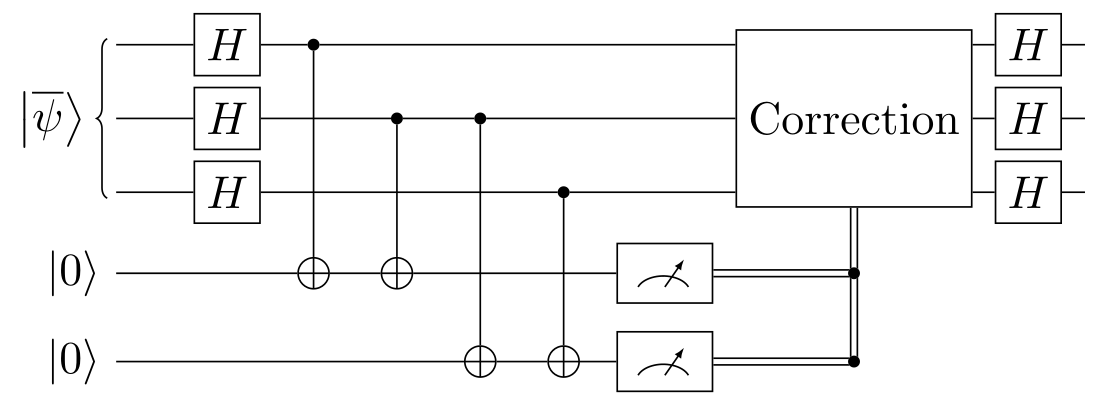 This system protects us against all single-qubit phase flips,
but not against bit flips.
## Shor code
What kind of repetition code would we need
if we want to detect both bit flips *and* phase flips?
The most straightforward option is the **Shor code**.
Starting from a phase flip encoding:
$$\begin{aligned}
\ket{0} \to
\ket*{\overline{0}}
&= \ket{+\!+\!+}
= \bigg( \frac{\ket{0} + \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\\
\ket{1} \to
\ket*{\overline{1}}
&= \ket{-\!-\!-}
= \bigg( \frac{\ket{0} - \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\end{aligned}$$
We add protection against bit flips
by using a repetition code for each physical qubit:
$$\begin{aligned}
\boxed{
\ket*{\overline{0}}
= \bigg( \frac{\ket{000} + \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
\qquad \quad
\ket*{\overline{1}}
= \bigg( \frac{\ket{000} - \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
}
\end{aligned}$$
This encoding is achieved by the following quantum circuit,
which simply consists of the phase flip encoder,
followed by 3 copies of the bit flip encoder:
This system protects us against all single-qubit phase flips,
but not against bit flips.
## Shor code
What kind of repetition code would we need
if we want to detect both bit flips *and* phase flips?
The most straightforward option is the **Shor code**.
Starting from a phase flip encoding:
$$\begin{aligned}
\ket{0} \to
\ket*{\overline{0}}
&= \ket{+\!+\!+}
= \bigg( \frac{\ket{0} + \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\\
\ket{1} \to
\ket*{\overline{1}}
&= \ket{-\!-\!-}
= \bigg( \frac{\ket{0} - \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\end{aligned}$$
We add protection against bit flips
by using a repetition code for each physical qubit:
$$\begin{aligned}
\boxed{
\ket*{\overline{0}}
= \bigg( \frac{\ket{000} + \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
\qquad \quad
\ket*{\overline{1}}
= \bigg( \frac{\ket{000} - \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
}
\end{aligned}$$
This encoding is achieved by the following quantum circuit,
which simply consists of the phase flip encoder,
followed by 3 copies of the bit flip encoder:
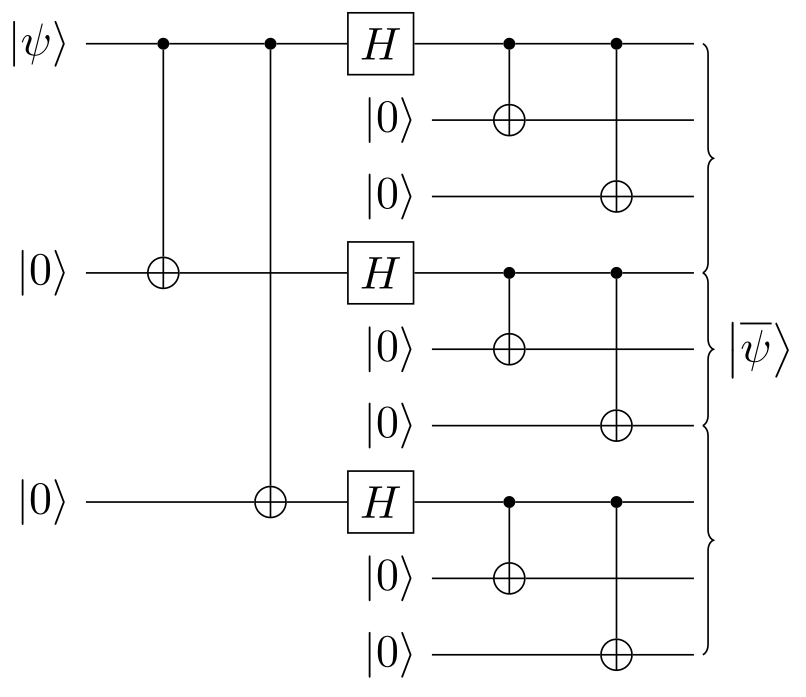 We thus use 9 physical qubits to store 1 logical qubit.
Fortunately, more efficient schemes exist.
The bit flip stabilizers $ZZI$ and $IZZ$
are applied on a per-block basis, like so:
$$\begin{aligned}
ZZI \: III \: III \qquad\quad III \: ZZI \: III \qquad\quad III \: III \: ZZI
\\
IZZ \: III \: III \qquad\quad III \: IZZ \: III \qquad\quad III \: III \: IZZ
\end{aligned}$$
Whereas the phase flip stabilizers $XXI$ and $IXX$
are applied to entire blocks at once:
$$\begin{aligned}
XXX \: XXX \: III
\qquad \quad
III \: XXX \: XXX
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
We thus use 9 physical qubits to store 1 logical qubit.
Fortunately, more efficient schemes exist.
The bit flip stabilizers $ZZI$ and $IZZ$
are applied on a per-block basis, like so:
$$\begin{aligned}
ZZI \: III \: III \qquad\quad III \: ZZI \: III \qquad\quad III \: III \: ZZI
\\
IZZ \: III \: III \qquad\quad III \: IZZ \: III \qquad\quad III \: III \: IZZ
\end{aligned}$$
Whereas the phase flip stabilizers $XXI$ and $IXX$
are applied to entire blocks at once:
$$\begin{aligned}
XXX \: XXX \: III
\qquad \quad
III \: XXX \: XXX
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
 So, a little while after encoding the state $\ket{\psi}$ like that,
a bit flip occurs on the 2nd qubit:
$$\begin{aligned}
\ket*{\overline{\psi}}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{010} + \beta \ket{101}
\end{aligned}$$
But now there is a problem: how do we detect this error?
We could measure the state, but that would make it collapse,
which is probably not what we want.
The trick is to use operators called **stabilizers**,
in this case for example $ZZI = Z_1 \otimes Z_2 \otimes I_3$,
where $I$ is identity and $Z$ is the Pauli-$Z$ gate.
The 3-qubit basis states are its eigenvectors:
$$\begin{alignedat}{2}
ZZI \ket{000}
&= + \ket{000}
\qquad
ZZI \ket{001}
&&= + \ket{001}
\\
ZZI \ket{010}
&= - \ket{010}
\qquad
ZZI \ket{011}
&&= - \ket{011}
\\
ZZI \ket{100}
&= - \ket{100}
\qquad
ZZI \ket{101}
&&= - \ket{101}
\\
ZZI \ket{110}
&= + \ket{110}
\qquad
ZZI \ket{111}
&&= + \ket{111}
\end{alignedat}$$
We could measure $ZZI$ for $\ket*{\overline{\psi}}$,
and if the eigenvalue is $-1$,
we know that a bit flip has occurred,
whereas if the eigenvalue is $+1$,
there is *maybe* no error ($\ket{001}$ and $\ket{110}$ are false negatives).
These false negatives are fixed by including another stabilizer $IZZ$,
with these eigenvectors:
$$\begin{alignedat}{2}
IZZ \ket{000}
&= + \ket{000}
\qquad
IZZ \ket{001}
&&= - \ket{001}
\\
IZZ \ket{010}
&= - \ket{010}
\qquad
IZZ \ket{011}
&&= + \ket{011}
\\
IZZ \ket{100}
&= + \ket{100}
\qquad
IZZ \ket{101}
&&= - \ket{101}
\\
IZZ \ket{110}
&= - \ket{110}
\qquad
IZZ \ket{111}
&&= + \ket{111}
\end{alignedat}$$
In which case $\ket{100}$ and $\ket{011}$ are false negatives.
In other words, $IZZ$ cannot detect if the 1st qubit was flipped,
while $ZZI$ cannot protect the 3rd qubit.
But by using both, we know exactly which qubit was flipped
thanks to the eigenvalues:
So, a little while after encoding the state $\ket{\psi}$ like that,
a bit flip occurs on the 2nd qubit:
$$\begin{aligned}
\ket*{\overline{\psi}}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{010} + \beta \ket{101}
\end{aligned}$$
But now there is a problem: how do we detect this error?
We could measure the state, but that would make it collapse,
which is probably not what we want.
The trick is to use operators called **stabilizers**,
in this case for example $ZZI = Z_1 \otimes Z_2 \otimes I_3$,
where $I$ is identity and $Z$ is the Pauli-$Z$ gate.
The 3-qubit basis states are its eigenvectors:
$$\begin{alignedat}{2}
ZZI \ket{000}
&= + \ket{000}
\qquad
ZZI \ket{001}
&&= + \ket{001}
\\
ZZI \ket{010}
&= - \ket{010}
\qquad
ZZI \ket{011}
&&= - \ket{011}
\\
ZZI \ket{100}
&= - \ket{100}
\qquad
ZZI \ket{101}
&&= - \ket{101}
\\
ZZI \ket{110}
&= + \ket{110}
\qquad
ZZI \ket{111}
&&= + \ket{111}
\end{alignedat}$$
We could measure $ZZI$ for $\ket*{\overline{\psi}}$,
and if the eigenvalue is $-1$,
we know that a bit flip has occurred,
whereas if the eigenvalue is $+1$,
there is *maybe* no error ($\ket{001}$ and $\ket{110}$ are false negatives).
These false negatives are fixed by including another stabilizer $IZZ$,
with these eigenvectors:
$$\begin{alignedat}{2}
IZZ \ket{000}
&= + \ket{000}
\qquad
IZZ \ket{001}
&&= - \ket{001}
\\
IZZ \ket{010}
&= - \ket{010}
\qquad
IZZ \ket{011}
&&= + \ket{011}
\\
IZZ \ket{100}
&= + \ket{100}
\qquad
IZZ \ket{101}
&&= - \ket{101}
\\
IZZ \ket{110}
&= - \ket{110}
\qquad
IZZ \ket{111}
&&= + \ket{111}
\end{alignedat}$$
In which case $\ket{100}$ and $\ket{011}$ are false negatives.
In other words, $IZZ$ cannot detect if the 1st qubit was flipped,
while $ZZI$ cannot protect the 3rd qubit.
But by using both, we know exactly which qubit was flipped
thanks to the eigenvalues:
 The two measurements, respectively representing $ZZI$ and $IZZ$,
yield $\ket{1}$ if a bit flip definitely occurred,
and $\ket{0}$ otherwise.
There is no entanglement,
so the input is untouched.
## Phase flip code
The above system protects us against all single-qubit bit flips.
Unfortunately, that is not enough:
qubits can also experience a **phase flip**:
$$\begin{aligned}
\alpha \ket{0} + \beta \ket{1}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{0} - \beta \ket{1}
\end{aligned}$$
How to detect that?
If we want to protect against phase flips *instead of* bit flips,
we can simply do the same as before,
but along the $X$-axis intead of the $Z$-axis:
$$\begin{aligned}
\boxed{
\ket{0}
\to
\ket*{\overline{0}}
= \ket{+\!+\!+}
\qquad \quad
\ket{1}
\to
\ket*{\overline{1}}
= \ket{-\!-\!-}
}
\end{aligned}$$
Such that an arbitrary state $\ket{\psi}$ is encoded as follows,
by the circuit shown below:
$$\begin{aligned}
\ket{\psi}
\quad \to \boxed{\mathrm{Encoder}} \to \quad
\ket*{\overline{\psi}}
= \alpha \ket{+\!+\!+} + \beta \ket{-\!-\!-}
\end{aligned}$$
The two measurements, respectively representing $ZZI$ and $IZZ$,
yield $\ket{1}$ if a bit flip definitely occurred,
and $\ket{0}$ otherwise.
There is no entanglement,
so the input is untouched.
## Phase flip code
The above system protects us against all single-qubit bit flips.
Unfortunately, that is not enough:
qubits can also experience a **phase flip**:
$$\begin{aligned}
\alpha \ket{0} + \beta \ket{1}
\quad \to \boxed{\mathrm{Error}} \to \quad
\alpha \ket{0} - \beta \ket{1}
\end{aligned}$$
How to detect that?
If we want to protect against phase flips *instead of* bit flips,
we can simply do the same as before,
but along the $X$-axis intead of the $Z$-axis:
$$\begin{aligned}
\boxed{
\ket{0}
\to
\ket*{\overline{0}}
= \ket{+\!+\!+}
\qquad \quad
\ket{1}
\to
\ket*{\overline{1}}
= \ket{-\!-\!-}
}
\end{aligned}$$
Such that an arbitrary state $\ket{\psi}$ is encoded as follows,
by the circuit shown below:
$$\begin{aligned}
\ket{\psi}
\quad \to \boxed{\mathrm{Encoder}} \to \quad
\ket*{\overline{\psi}}
= \alpha \ket{+\!+\!+} + \beta \ket{-\!-\!-}
\end{aligned}$$
 A phase flip along the $Z$-axis
corresponds to a bit flip along the $X$-axis $\ket{+} \to \ket{-}$.
In this case, the stabilizers are $XXI$ and $IXX$,
and the error detection circuit is as follows:
A phase flip along the $Z$-axis
corresponds to a bit flip along the $X$-axis $\ket{+} \to \ket{-}$.
In this case, the stabilizers are $XXI$ and $IXX$,
and the error detection circuit is as follows:
 This system protects us against all single-qubit phase flips,
but not against bit flips.
## Shor code
What kind of repetition code would we need
if we want to detect both bit flips *and* phase flips?
The most straightforward option is the **Shor code**.
Starting from a phase flip encoding:
$$\begin{aligned}
\ket{0} \to
\ket*{\overline{0}}
&= \ket{+\!+\!+}
= \bigg( \frac{\ket{0} + \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\\
\ket{1} \to
\ket*{\overline{1}}
&= \ket{-\!-\!-}
= \bigg( \frac{\ket{0} - \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\end{aligned}$$
We add protection against bit flips
by using a repetition code for each physical qubit:
$$\begin{aligned}
\boxed{
\ket*{\overline{0}}
= \bigg( \frac{\ket{000} + \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
\qquad \quad
\ket*{\overline{1}}
= \bigg( \frac{\ket{000} - \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
}
\end{aligned}$$
This encoding is achieved by the following quantum circuit,
which simply consists of the phase flip encoder,
followed by 3 copies of the bit flip encoder:
This system protects us against all single-qubit phase flips,
but not against bit flips.
## Shor code
What kind of repetition code would we need
if we want to detect both bit flips *and* phase flips?
The most straightforward option is the **Shor code**.
Starting from a phase flip encoding:
$$\begin{aligned}
\ket{0} \to
\ket*{\overline{0}}
&= \ket{+\!+\!+}
= \bigg( \frac{\ket{0} + \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\\
\ket{1} \to
\ket*{\overline{1}}
&= \ket{-\!-\!-}
= \bigg( \frac{\ket{0} - \ket{1}}{\sqrt{2}} \bigg)^{\otimes 3}
\end{aligned}$$
We add protection against bit flips
by using a repetition code for each physical qubit:
$$\begin{aligned}
\boxed{
\ket*{\overline{0}}
= \bigg( \frac{\ket{000} + \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
\qquad \quad
\ket*{\overline{1}}
= \bigg( \frac{\ket{000} - \ket{111}}{\sqrt{2}} \bigg)^{\otimes 3}
}
\end{aligned}$$
This encoding is achieved by the following quantum circuit,
which simply consists of the phase flip encoder,
followed by 3 copies of the bit flip encoder:
 We thus use 9 physical qubits to store 1 logical qubit.
Fortunately, more efficient schemes exist.
The bit flip stabilizers $ZZI$ and $IZZ$
are applied on a per-block basis, like so:
$$\begin{aligned}
ZZI \: III \: III \qquad\quad III \: ZZI \: III \qquad\quad III \: III \: ZZI
\\
IZZ \: III \: III \qquad\quad III \: IZZ \: III \qquad\quad III \: III \: IZZ
\end{aligned}$$
Whereas the phase flip stabilizers $XXI$ and $IXX$
are applied to entire blocks at once:
$$\begin{aligned}
XXX \: XXX \: III
\qquad \quad
III \: XXX \: XXX
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
We thus use 9 physical qubits to store 1 logical qubit.
Fortunately, more efficient schemes exist.
The bit flip stabilizers $ZZI$ and $IZZ$
are applied on a per-block basis, like so:
$$\begin{aligned}
ZZI \: III \: III \qquad\quad III \: ZZI \: III \qquad\quad III \: III \: ZZI
\\
IZZ \: III \: III \qquad\quad III \: IZZ \: III \qquad\quad III \: III \: IZZ
\end{aligned}$$
Whereas the phase flip stabilizers $XXI$ and $IXX$
are applied to entire blocks at once:
$$\begin{aligned}
XXX \: XXX \: III
\qquad \quad
III \: XXX \: XXX
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.