---
title: "Rutherford scattering"
firstLetter: "R"
publishDate: 2021-10-02
categories:
- Physics
- Plasma physics
date: 2021-09-23T16:22:07+02:00
draft: false
markup: pandoc
---
# Rutherford scattering
**Rutherford scattering** or **Coulomb scattering**
is an elastic pseudo-collision of two electrically charged particles.
It is not a true collision, and is caused by Coulomb repulsion.
The general idea is illustrated below.
Consider two particles 1 and 2, with the same charge sign.
Let 2 be initially at rest, and 1 approach it with velocity $\vb{v}_1$.
Coulomb repulsion causes 1 to deflect by an angle $\theta$,
and pushes 2 away in the process:
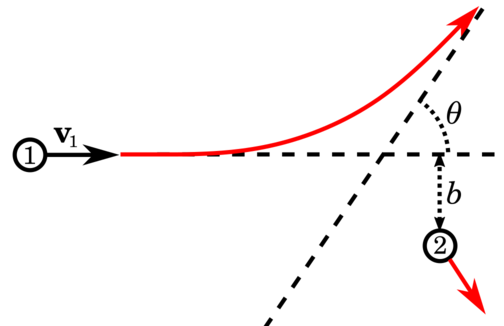 Here, $b$ is called the **impact parameter**.
Intuitively, we expect $\theta$ to be larger for smaller $b$.
By combining Coulomb's law with Newton's laws,
these particles' equations of motion are found to be as follows,
where $r = |\vb{r}_1 - \vb{r}_2|$ is the distance between 1 and 2:
$$\begin{aligned}
m_1 \dv{\vb{v}_1}{t}
= \vb{F}_1
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}_1 - \vb{r}_2}{r^3}
\qquad \quad
m_2 \dv{\vb{v}_2}{t}
= \vb{F}_2
= - \vb{F}_1
\end{aligned}$$
Using the [reduced mass](/know/concept/reduced-mass/)
$\mu \equiv m_1 m_2 / (m_1 \!+\! m_2)$,
we turn this into a one-body problem:
$$\begin{aligned}
\mu \dv{\vb{v}}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3}
\end{aligned}$$
Where $\vb{v} \equiv \vb{v}_1 \!-\! \vb{v}_2$ is the relative velocity,
and $\vb{r} \equiv \vb{r}_1 \!-\! \vb{r}_2$ is the relative position.
The latter is as follows in
[cylindrical polar coordinates](/know/concept/cylindrical-polar-coordinates/)
$(r, \varphi, z)$:
$$\begin{aligned}
\vb{r}
= r \cos{\varphi} \:\vu{e}_x + r \sin{\varphi} \:\vu{e}_y + z \:\vu{e}_z
= r \:\vu{e}_r + z \:\vu{e}_z
\end{aligned}$$
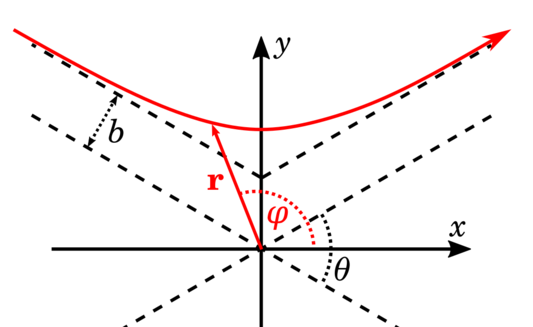
These new coordinates are sketched below,
where the origin represents $\vb{r}_1 = \vb{r}_2$.
Crucially, note the symmetry:
if the "collision" occurs at $t = 0$,
then by comparing $t > 0$ and $t < 0$
we can see that $v_x$ is unchanged for any given $\pm t$,
while $v_y$ simply changes sign:
Here, $b$ is called the **impact parameter**.
Intuitively, we expect $\theta$ to be larger for smaller $b$.
By combining Coulomb's law with Newton's laws,
these particles' equations of motion are found to be as follows,
where $r = |\vb{r}_1 - \vb{r}_2|$ is the distance between 1 and 2:
$$\begin{aligned}
m_1 \dv{\vb{v}_1}{t}
= \vb{F}_1
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}_1 - \vb{r}_2}{r^3}
\qquad \quad
m_2 \dv{\vb{v}_2}{t}
= \vb{F}_2
= - \vb{F}_1
\end{aligned}$$
Using the [reduced mass](/know/concept/reduced-mass/)
$\mu \equiv m_1 m_2 / (m_1 \!+\! m_2)$,
we turn this into a one-body problem:
$$\begin{aligned}
\mu \dv{\vb{v}}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3}
\end{aligned}$$
Where $\vb{v} \equiv \vb{v}_1 \!-\! \vb{v}_2$ is the relative velocity,
and $\vb{r} \equiv \vb{r}_1 \!-\! \vb{r}_2$ is the relative position.
The latter is as follows in
[cylindrical polar coordinates](/know/concept/cylindrical-polar-coordinates/)
$(r, \varphi, z)$:
$$\begin{aligned}
\vb{r}
= r \cos{\varphi} \:\vu{e}_x + r \sin{\varphi} \:\vu{e}_y + z \:\vu{e}_z
= r \:\vu{e}_r + z \:\vu{e}_z
\end{aligned}$$
These new coordinates are sketched below,
where the origin represents $\vb{r}_1 = \vb{r}_2$.
Crucially, note the symmetry:
if the "collision" occurs at $t = 0$,
then by comparing $t > 0$ and $t < 0$
we can see that $v_x$ is unchanged for any given $\pm t$,
while $v_y$ simply changes sign:
 From our expression for $\vb{r}$,
we can find $\vb{v}$ by differentiating with respect to time:
$$\begin{aligned}
\vb{v}
&= \big( r' \cos{\varphi} - r \varphi' \sin{\varphi} \big) \:\vu{e}_x
+ \big( r' \sin{\varphi} + r \varphi' \cos{\varphi} \big) \:\vu{e}_y + z' \:\vu{e}_z
\\
&= r' \: \big( \cos{\varphi} \:\vu{e}_x + \sin{\varphi} \:\vu{e}_y \big)
+ r \varphi' \: \big( \!-\! \sin{\varphi} \:\vu{e}_x + \cos{\varphi} \:\vu{e}_y \big) + z' \:\vu{e}_z
\\
&= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi + z' \:\vu{e}_z
\end{aligned}$$
Where we have recognized the basis vectors $\vu{e}_r$ and $\vu{e}_\varphi$.
If we choose the coordinate system such that all dynamics are in the $(x,y)$-plane,
i.e. $z(t) = 0$, we have:
$$\begin{aligned}
\vb{r}
= r \: \vu{e}_r
\qquad \qquad
\vb{v}
= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi
\end{aligned}$$
Consequently, the angular momentum $\vb{L}$ is as follows,
pointing purely in the $z$-direction:
$$\begin{aligned}
\vb{L}(t)
= \mu \vb{r} \cross \vb{v}
= \mu \big( r \vu{e}_r \cross r \varphi' \vu{e}_\varphi \big)
= \mu r^2 \varphi' \:\vu{e}_z
\end{aligned}$$
Now, from the figure above,
we can argue geometrically that at infinity $t = \pm \infty$,
the ratio $b/r$ is related to the angle $\chi$ between $\vb{v}$ and $\vb{r}$ like so:
$$\begin{aligned}
\frac{b}{r(\pm \infty)}
= \sin{\chi(\pm \infty)}
\qquad \quad
\chi(t)
\equiv \measuredangle(\vb{r}, \vb{v})
\end{aligned}$$
With this, we can rewrite
the magnitude of the angular momentum $\vb{L}$ as follows,
where the total velocity $|\vb{v}|$ is a constant,
thanks to conservation of energy:
$$\begin{aligned}
\big| \vb{L}(\pm \infty) \big|
= \mu \big| \vb{r} \cross \vb{v} \big|
= \mu r |\vb{v}| \sin{\chi}
= \mu b |\vb{v}|
\end{aligned}$$
However, conveniently,
angular momentum is also conserved, i.e. $\vb{L}$ is constant in time:
$$\begin{aligned}
\vb{L}'(t)
&= \mu \big( \vb{r} \cross \vb{v}' + \vb{v} \cross \vb{v} \big)
= \vb{r} \cross (\mu \vb{v}')
= \vb{r} \cross \Big( \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3} \Big)
= 0
\end{aligned}$$
Where we have replaced $\mu \vb{v}'$ with the equation of motion.
Thanks to this, we can equate the two preceding expressions for $\vb{L}$,
leading to the relation below.
Note the appearance of a new minus,
because the sketch shows that $\varphi' < 0$,
i.e. $\varphi$ decreases with increasing $t$:
$$\begin{aligned}
- \mu r^2 \dv{\varphi}{t}
= \mu b |\vb{v}|
\quad \implies \quad
\dd{t}
= - \frac{r^2}{b |\vb{v}|} \dd{\varphi}
\end{aligned}$$
Now, at last, we turn to the main equation of motion.
Its $y$-component is given by:
$$\begin{aligned}
\mu \dv{v_y}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3}
\quad \implies \quad
\mu \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3} \dd{t}
\end{aligned}$$
We replace $\dd{t}$ with our earlier relation,
and recognize geometrically that $y/r = \sin{\varphi}$:
$$\begin{aligned}
\mu \dd{v_y}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \frac{y}{r} \dd{\varphi}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \sin{\varphi} \dd{\varphi}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \dd{(\cos{\varphi})}
\end{aligned}$$
Integrating this from the initial state $i$ at $t = -\infty$
to the final state $f$ at $t = \infty$ yields:
$$\begin{aligned}
\Delta v_y
\equiv \int_{i}^{f} \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos{\varphi_i} \big)
\end{aligned}$$
From symmetry, we see that $\varphi_i = \pi \!-\! \varphi_f$,
and that $\Delta v_y = v_{y,f} \!-\! v_{y,i} = 2 v_{y,f}$, such that:
$$\begin{aligned}
2 v_{y,f}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos\!(\pi \!-\! \varphi_f) \big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( 2 \cos{\varphi_f} \big)
\end{aligned}$$
Furthermore, geometrically, at $t = \infty$
we notice that $v_{y,f} = |\vb{v}| \sin{\varphi_f}$,
leading to:
$$\begin{aligned}
2 |\vb{v}| \sin{\varphi_f}
= \frac{q_1 q_2}{2 \pi \varepsilon_0 b |\vb{v}| \mu} \cos{\varphi_f}
\end{aligned}$$
Rearranging this yields the following equation
for the final polar angle $\varphi_f \equiv \varphi(\infty)$:
$$\begin{aligned}
\tan{\varphi_f}
= \frac{\sin{\varphi_f}}{\cos{\varphi_f}}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
\end{aligned}$$
However, we want $\theta$, not $\varphi_f$.
One last use of symmetry and geometry
tells us that $\theta = 2 \varphi_f$,
and we thus arrive at the celebrated **Rutherford scattering formula**:
$$\begin{aligned}
\boxed{
\tan\!\Big( \frac{\theta}{2} \Big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
}
\end{aligned}$$
In fact, this formula is also valid if $q_1$ and $q_2$ have opposite signs;
in that case particle 2 is simply located on the other side
of particle 1's trajectory.
## References
1. P.M. Bellan,
*Fundamentals of plasma physics*,
1st edition, Cambridge.
2. M. Salewski, A.H. Nielsen,
*Plasma physics: lecture notes*,
2021, unpublished.
From our expression for $\vb{r}$,
we can find $\vb{v}$ by differentiating with respect to time:
$$\begin{aligned}
\vb{v}
&= \big( r' \cos{\varphi} - r \varphi' \sin{\varphi} \big) \:\vu{e}_x
+ \big( r' \sin{\varphi} + r \varphi' \cos{\varphi} \big) \:\vu{e}_y + z' \:\vu{e}_z
\\
&= r' \: \big( \cos{\varphi} \:\vu{e}_x + \sin{\varphi} \:\vu{e}_y \big)
+ r \varphi' \: \big( \!-\! \sin{\varphi} \:\vu{e}_x + \cos{\varphi} \:\vu{e}_y \big) + z' \:\vu{e}_z
\\
&= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi + z' \:\vu{e}_z
\end{aligned}$$
Where we have recognized the basis vectors $\vu{e}_r$ and $\vu{e}_\varphi$.
If we choose the coordinate system such that all dynamics are in the $(x,y)$-plane,
i.e. $z(t) = 0$, we have:
$$\begin{aligned}
\vb{r}
= r \: \vu{e}_r
\qquad \qquad
\vb{v}
= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi
\end{aligned}$$
Consequently, the angular momentum $\vb{L}$ is as follows,
pointing purely in the $z$-direction:
$$\begin{aligned}
\vb{L}(t)
= \mu \vb{r} \cross \vb{v}
= \mu \big( r \vu{e}_r \cross r \varphi' \vu{e}_\varphi \big)
= \mu r^2 \varphi' \:\vu{e}_z
\end{aligned}$$
Now, from the figure above,
we can argue geometrically that at infinity $t = \pm \infty$,
the ratio $b/r$ is related to the angle $\chi$ between $\vb{v}$ and $\vb{r}$ like so:
$$\begin{aligned}
\frac{b}{r(\pm \infty)}
= \sin{\chi(\pm \infty)}
\qquad \quad
\chi(t)
\equiv \measuredangle(\vb{r}, \vb{v})
\end{aligned}$$
With this, we can rewrite
the magnitude of the angular momentum $\vb{L}$ as follows,
where the total velocity $|\vb{v}|$ is a constant,
thanks to conservation of energy:
$$\begin{aligned}
\big| \vb{L}(\pm \infty) \big|
= \mu \big| \vb{r} \cross \vb{v} \big|
= \mu r |\vb{v}| \sin{\chi}
= \mu b |\vb{v}|
\end{aligned}$$
However, conveniently,
angular momentum is also conserved, i.e. $\vb{L}$ is constant in time:
$$\begin{aligned}
\vb{L}'(t)
&= \mu \big( \vb{r} \cross \vb{v}' + \vb{v} \cross \vb{v} \big)
= \vb{r} \cross (\mu \vb{v}')
= \vb{r} \cross \Big( \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3} \Big)
= 0
\end{aligned}$$
Where we have replaced $\mu \vb{v}'$ with the equation of motion.
Thanks to this, we can equate the two preceding expressions for $\vb{L}$,
leading to the relation below.
Note the appearance of a new minus,
because the sketch shows that $\varphi' < 0$,
i.e. $\varphi$ decreases with increasing $t$:
$$\begin{aligned}
- \mu r^2 \dv{\varphi}{t}
= \mu b |\vb{v}|
\quad \implies \quad
\dd{t}
= - \frac{r^2}{b |\vb{v}|} \dd{\varphi}
\end{aligned}$$
Now, at last, we turn to the main equation of motion.
Its $y$-component is given by:
$$\begin{aligned}
\mu \dv{v_y}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3}
\quad \implies \quad
\mu \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3} \dd{t}
\end{aligned}$$
We replace $\dd{t}$ with our earlier relation,
and recognize geometrically that $y/r = \sin{\varphi}$:
$$\begin{aligned}
\mu \dd{v_y}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \frac{y}{r} \dd{\varphi}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \sin{\varphi} \dd{\varphi}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \dd{(\cos{\varphi})}
\end{aligned}$$
Integrating this from the initial state $i$ at $t = -\infty$
to the final state $f$ at $t = \infty$ yields:
$$\begin{aligned}
\Delta v_y
\equiv \int_{i}^{f} \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos{\varphi_i} \big)
\end{aligned}$$
From symmetry, we see that $\varphi_i = \pi \!-\! \varphi_f$,
and that $\Delta v_y = v_{y,f} \!-\! v_{y,i} = 2 v_{y,f}$, such that:
$$\begin{aligned}
2 v_{y,f}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos\!(\pi \!-\! \varphi_f) \big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( 2 \cos{\varphi_f} \big)
\end{aligned}$$
Furthermore, geometrically, at $t = \infty$
we notice that $v_{y,f} = |\vb{v}| \sin{\varphi_f}$,
leading to:
$$\begin{aligned}
2 |\vb{v}| \sin{\varphi_f}
= \frac{q_1 q_2}{2 \pi \varepsilon_0 b |\vb{v}| \mu} \cos{\varphi_f}
\end{aligned}$$
Rearranging this yields the following equation
for the final polar angle $\varphi_f \equiv \varphi(\infty)$:
$$\begin{aligned}
\tan{\varphi_f}
= \frac{\sin{\varphi_f}}{\cos{\varphi_f}}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
\end{aligned}$$
However, we want $\theta$, not $\varphi_f$.
One last use of symmetry and geometry
tells us that $\theta = 2 \varphi_f$,
and we thus arrive at the celebrated **Rutherford scattering formula**:
$$\begin{aligned}
\boxed{
\tan\!\Big( \frac{\theta}{2} \Big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
}
\end{aligned}$$
In fact, this formula is also valid if $q_1$ and $q_2$ have opposite signs;
in that case particle 2 is simply located on the other side
of particle 1's trajectory.
## References
1. P.M. Bellan,
*Fundamentals of plasma physics*,
1st edition, Cambridge.
2. M. Salewski, A.H. Nielsen,
*Plasma physics: lecture notes*,
2021, unpublished.
 Here, $b$ is called the **impact parameter**.
Intuitively, we expect $\theta$ to be larger for smaller $b$.
By combining Coulomb's law with Newton's laws,
these particles' equations of motion are found to be as follows,
where $r = |\vb{r}_1 - \vb{r}_2|$ is the distance between 1 and 2:
$$\begin{aligned}
m_1 \dv{\vb{v}_1}{t}
= \vb{F}_1
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}_1 - \vb{r}_2}{r^3}
\qquad \quad
m_2 \dv{\vb{v}_2}{t}
= \vb{F}_2
= - \vb{F}_1
\end{aligned}$$
Using the [reduced mass](/know/concept/reduced-mass/)
$\mu \equiv m_1 m_2 / (m_1 \!+\! m_2)$,
we turn this into a one-body problem:
$$\begin{aligned}
\mu \dv{\vb{v}}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3}
\end{aligned}$$
Where $\vb{v} \equiv \vb{v}_1 \!-\! \vb{v}_2$ is the relative velocity,
and $\vb{r} \equiv \vb{r}_1 \!-\! \vb{r}_2$ is the relative position.
The latter is as follows in
[cylindrical polar coordinates](/know/concept/cylindrical-polar-coordinates/)
$(r, \varphi, z)$:
$$\begin{aligned}
\vb{r}
= r \cos{\varphi} \:\vu{e}_x + r \sin{\varphi} \:\vu{e}_y + z \:\vu{e}_z
= r \:\vu{e}_r + z \:\vu{e}_z
\end{aligned}$$
These new coordinates are sketched below,
where the origin represents $\vb{r}_1 = \vb{r}_2$.
Crucially, note the symmetry:
if the "collision" occurs at $t = 0$,
then by comparing $t > 0$ and $t < 0$
we can see that $v_x$ is unchanged for any given $\pm t$,
while $v_y$ simply changes sign:
Here, $b$ is called the **impact parameter**.
Intuitively, we expect $\theta$ to be larger for smaller $b$.
By combining Coulomb's law with Newton's laws,
these particles' equations of motion are found to be as follows,
where $r = |\vb{r}_1 - \vb{r}_2|$ is the distance between 1 and 2:
$$\begin{aligned}
m_1 \dv{\vb{v}_1}{t}
= \vb{F}_1
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}_1 - \vb{r}_2}{r^3}
\qquad \quad
m_2 \dv{\vb{v}_2}{t}
= \vb{F}_2
= - \vb{F}_1
\end{aligned}$$
Using the [reduced mass](/know/concept/reduced-mass/)
$\mu \equiv m_1 m_2 / (m_1 \!+\! m_2)$,
we turn this into a one-body problem:
$$\begin{aligned}
\mu \dv{\vb{v}}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3}
\end{aligned}$$
Where $\vb{v} \equiv \vb{v}_1 \!-\! \vb{v}_2$ is the relative velocity,
and $\vb{r} \equiv \vb{r}_1 \!-\! \vb{r}_2$ is the relative position.
The latter is as follows in
[cylindrical polar coordinates](/know/concept/cylindrical-polar-coordinates/)
$(r, \varphi, z)$:
$$\begin{aligned}
\vb{r}
= r \cos{\varphi} \:\vu{e}_x + r \sin{\varphi} \:\vu{e}_y + z \:\vu{e}_z
= r \:\vu{e}_r + z \:\vu{e}_z
\end{aligned}$$
These new coordinates are sketched below,
where the origin represents $\vb{r}_1 = \vb{r}_2$.
Crucially, note the symmetry:
if the "collision" occurs at $t = 0$,
then by comparing $t > 0$ and $t < 0$
we can see that $v_x$ is unchanged for any given $\pm t$,
while $v_y$ simply changes sign:
 From our expression for $\vb{r}$,
we can find $\vb{v}$ by differentiating with respect to time:
$$\begin{aligned}
\vb{v}
&= \big( r' \cos{\varphi} - r \varphi' \sin{\varphi} \big) \:\vu{e}_x
+ \big( r' \sin{\varphi} + r \varphi' \cos{\varphi} \big) \:\vu{e}_y + z' \:\vu{e}_z
\\
&= r' \: \big( \cos{\varphi} \:\vu{e}_x + \sin{\varphi} \:\vu{e}_y \big)
+ r \varphi' \: \big( \!-\! \sin{\varphi} \:\vu{e}_x + \cos{\varphi} \:\vu{e}_y \big) + z' \:\vu{e}_z
\\
&= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi + z' \:\vu{e}_z
\end{aligned}$$
Where we have recognized the basis vectors $\vu{e}_r$ and $\vu{e}_\varphi$.
If we choose the coordinate system such that all dynamics are in the $(x,y)$-plane,
i.e. $z(t) = 0$, we have:
$$\begin{aligned}
\vb{r}
= r \: \vu{e}_r
\qquad \qquad
\vb{v}
= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi
\end{aligned}$$
Consequently, the angular momentum $\vb{L}$ is as follows,
pointing purely in the $z$-direction:
$$\begin{aligned}
\vb{L}(t)
= \mu \vb{r} \cross \vb{v}
= \mu \big( r \vu{e}_r \cross r \varphi' \vu{e}_\varphi \big)
= \mu r^2 \varphi' \:\vu{e}_z
\end{aligned}$$
Now, from the figure above,
we can argue geometrically that at infinity $t = \pm \infty$,
the ratio $b/r$ is related to the angle $\chi$ between $\vb{v}$ and $\vb{r}$ like so:
$$\begin{aligned}
\frac{b}{r(\pm \infty)}
= \sin{\chi(\pm \infty)}
\qquad \quad
\chi(t)
\equiv \measuredangle(\vb{r}, \vb{v})
\end{aligned}$$
With this, we can rewrite
the magnitude of the angular momentum $\vb{L}$ as follows,
where the total velocity $|\vb{v}|$ is a constant,
thanks to conservation of energy:
$$\begin{aligned}
\big| \vb{L}(\pm \infty) \big|
= \mu \big| \vb{r} \cross \vb{v} \big|
= \mu r |\vb{v}| \sin{\chi}
= \mu b |\vb{v}|
\end{aligned}$$
However, conveniently,
angular momentum is also conserved, i.e. $\vb{L}$ is constant in time:
$$\begin{aligned}
\vb{L}'(t)
&= \mu \big( \vb{r} \cross \vb{v}' + \vb{v} \cross \vb{v} \big)
= \vb{r} \cross (\mu \vb{v}')
= \vb{r} \cross \Big( \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3} \Big)
= 0
\end{aligned}$$
Where we have replaced $\mu \vb{v}'$ with the equation of motion.
Thanks to this, we can equate the two preceding expressions for $\vb{L}$,
leading to the relation below.
Note the appearance of a new minus,
because the sketch shows that $\varphi' < 0$,
i.e. $\varphi$ decreases with increasing $t$:
$$\begin{aligned}
- \mu r^2 \dv{\varphi}{t}
= \mu b |\vb{v}|
\quad \implies \quad
\dd{t}
= - \frac{r^2}{b |\vb{v}|} \dd{\varphi}
\end{aligned}$$
Now, at last, we turn to the main equation of motion.
Its $y$-component is given by:
$$\begin{aligned}
\mu \dv{v_y}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3}
\quad \implies \quad
\mu \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3} \dd{t}
\end{aligned}$$
We replace $\dd{t}$ with our earlier relation,
and recognize geometrically that $y/r = \sin{\varphi}$:
$$\begin{aligned}
\mu \dd{v_y}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \frac{y}{r} \dd{\varphi}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \sin{\varphi} \dd{\varphi}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \dd{(\cos{\varphi})}
\end{aligned}$$
Integrating this from the initial state $i$ at $t = -\infty$
to the final state $f$ at $t = \infty$ yields:
$$\begin{aligned}
\Delta v_y
\equiv \int_{i}^{f} \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos{\varphi_i} \big)
\end{aligned}$$
From symmetry, we see that $\varphi_i = \pi \!-\! \varphi_f$,
and that $\Delta v_y = v_{y,f} \!-\! v_{y,i} = 2 v_{y,f}$, such that:
$$\begin{aligned}
2 v_{y,f}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos\!(\pi \!-\! \varphi_f) \big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( 2 \cos{\varphi_f} \big)
\end{aligned}$$
Furthermore, geometrically, at $t = \infty$
we notice that $v_{y,f} = |\vb{v}| \sin{\varphi_f}$,
leading to:
$$\begin{aligned}
2 |\vb{v}| \sin{\varphi_f}
= \frac{q_1 q_2}{2 \pi \varepsilon_0 b |\vb{v}| \mu} \cos{\varphi_f}
\end{aligned}$$
Rearranging this yields the following equation
for the final polar angle $\varphi_f \equiv \varphi(\infty)$:
$$\begin{aligned}
\tan{\varphi_f}
= \frac{\sin{\varphi_f}}{\cos{\varphi_f}}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
\end{aligned}$$
However, we want $\theta$, not $\varphi_f$.
One last use of symmetry and geometry
tells us that $\theta = 2 \varphi_f$,
and we thus arrive at the celebrated **Rutherford scattering formula**:
$$\begin{aligned}
\boxed{
\tan\!\Big( \frac{\theta}{2} \Big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
}
\end{aligned}$$
In fact, this formula is also valid if $q_1$ and $q_2$ have opposite signs;
in that case particle 2 is simply located on the other side
of particle 1's trajectory.
## References
1. P.M. Bellan,
*Fundamentals of plasma physics*,
1st edition, Cambridge.
2. M. Salewski, A.H. Nielsen,
*Plasma physics: lecture notes*,
2021, unpublished.
From our expression for $\vb{r}$,
we can find $\vb{v}$ by differentiating with respect to time:
$$\begin{aligned}
\vb{v}
&= \big( r' \cos{\varphi} - r \varphi' \sin{\varphi} \big) \:\vu{e}_x
+ \big( r' \sin{\varphi} + r \varphi' \cos{\varphi} \big) \:\vu{e}_y + z' \:\vu{e}_z
\\
&= r' \: \big( \cos{\varphi} \:\vu{e}_x + \sin{\varphi} \:\vu{e}_y \big)
+ r \varphi' \: \big( \!-\! \sin{\varphi} \:\vu{e}_x + \cos{\varphi} \:\vu{e}_y \big) + z' \:\vu{e}_z
\\
&= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi + z' \:\vu{e}_z
\end{aligned}$$
Where we have recognized the basis vectors $\vu{e}_r$ and $\vu{e}_\varphi$.
If we choose the coordinate system such that all dynamics are in the $(x,y)$-plane,
i.e. $z(t) = 0$, we have:
$$\begin{aligned}
\vb{r}
= r \: \vu{e}_r
\qquad \qquad
\vb{v}
= r' \:\vu{e}_r + r \varphi' \:\vu{e}_\varphi
\end{aligned}$$
Consequently, the angular momentum $\vb{L}$ is as follows,
pointing purely in the $z$-direction:
$$\begin{aligned}
\vb{L}(t)
= \mu \vb{r} \cross \vb{v}
= \mu \big( r \vu{e}_r \cross r \varphi' \vu{e}_\varphi \big)
= \mu r^2 \varphi' \:\vu{e}_z
\end{aligned}$$
Now, from the figure above,
we can argue geometrically that at infinity $t = \pm \infty$,
the ratio $b/r$ is related to the angle $\chi$ between $\vb{v}$ and $\vb{r}$ like so:
$$\begin{aligned}
\frac{b}{r(\pm \infty)}
= \sin{\chi(\pm \infty)}
\qquad \quad
\chi(t)
\equiv \measuredangle(\vb{r}, \vb{v})
\end{aligned}$$
With this, we can rewrite
the magnitude of the angular momentum $\vb{L}$ as follows,
where the total velocity $|\vb{v}|$ is a constant,
thanks to conservation of energy:
$$\begin{aligned}
\big| \vb{L}(\pm \infty) \big|
= \mu \big| \vb{r} \cross \vb{v} \big|
= \mu r |\vb{v}| \sin{\chi}
= \mu b |\vb{v}|
\end{aligned}$$
However, conveniently,
angular momentum is also conserved, i.e. $\vb{L}$ is constant in time:
$$\begin{aligned}
\vb{L}'(t)
&= \mu \big( \vb{r} \cross \vb{v}' + \vb{v} \cross \vb{v} \big)
= \vb{r} \cross (\mu \vb{v}')
= \vb{r} \cross \Big( \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{\vb{r}}{r^3} \Big)
= 0
\end{aligned}$$
Where we have replaced $\mu \vb{v}'$ with the equation of motion.
Thanks to this, we can equate the two preceding expressions for $\vb{L}$,
leading to the relation below.
Note the appearance of a new minus,
because the sketch shows that $\varphi' < 0$,
i.e. $\varphi$ decreases with increasing $t$:
$$\begin{aligned}
- \mu r^2 \dv{\varphi}{t}
= \mu b |\vb{v}|
\quad \implies \quad
\dd{t}
= - \frac{r^2}{b |\vb{v}|} \dd{\varphi}
\end{aligned}$$
Now, at last, we turn to the main equation of motion.
Its $y$-component is given by:
$$\begin{aligned}
\mu \dv{v_y}{t}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3}
\quad \implies \quad
\mu \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{y}{r^3} \dd{t}
\end{aligned}$$
We replace $\dd{t}$ with our earlier relation,
and recognize geometrically that $y/r = \sin{\varphi}$:
$$\begin{aligned}
\mu \dd{v_y}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \frac{y}{r} \dd{\varphi}
= - \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \sin{\varphi} \dd{\varphi}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|} \dd{(\cos{\varphi})}
\end{aligned}$$
Integrating this from the initial state $i$ at $t = -\infty$
to the final state $f$ at $t = \infty$ yields:
$$\begin{aligned}
\Delta v_y
\equiv \int_{i}^{f} \dd{v_y}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos{\varphi_i} \big)
\end{aligned}$$
From symmetry, we see that $\varphi_i = \pi \!-\! \varphi_f$,
and that $\Delta v_y = v_{y,f} \!-\! v_{y,i} = 2 v_{y,f}$, such that:
$$\begin{aligned}
2 v_{y,f}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( \cos{\varphi_f} - \cos\!(\pi \!-\! \varphi_f) \big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}| \mu} \big( 2 \cos{\varphi_f} \big)
\end{aligned}$$
Furthermore, geometrically, at $t = \infty$
we notice that $v_{y,f} = |\vb{v}| \sin{\varphi_f}$,
leading to:
$$\begin{aligned}
2 |\vb{v}| \sin{\varphi_f}
= \frac{q_1 q_2}{2 \pi \varepsilon_0 b |\vb{v}| \mu} \cos{\varphi_f}
\end{aligned}$$
Rearranging this yields the following equation
for the final polar angle $\varphi_f \equiv \varphi(\infty)$:
$$\begin{aligned}
\tan{\varphi_f}
= \frac{\sin{\varphi_f}}{\cos{\varphi_f}}
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
\end{aligned}$$
However, we want $\theta$, not $\varphi_f$.
One last use of symmetry and geometry
tells us that $\theta = 2 \varphi_f$,
and we thus arrive at the celebrated **Rutherford scattering formula**:
$$\begin{aligned}
\boxed{
\tan\!\Big( \frac{\theta}{2} \Big)
= \frac{q_1 q_2}{4 \pi \varepsilon_0 b |\vb{v}|^2 \mu}
}
\end{aligned}$$
In fact, this formula is also valid if $q_1$ and $q_2$ have opposite signs;
in that case particle 2 is simply located on the other side
of particle 1's trajectory.
## References
1. P.M. Bellan,
*Fundamentals of plasma physics*,
1st edition, Cambridge.
2. M. Salewski, A.H. Nielsen,
*Plasma physics: lecture notes*,
2021, unpublished.