---
title: "Toffoli gate"
firstLetter: "T"
publishDate: 2021-04-09
categories:
- Quantum information
date: 2021-04-09T14:44:43+02:00
draft: false
markup: pandoc
---
# Toffoli gate
The **Toffoli gate** or **controlled-controlled-NOT (CCNOT) gate**
is a logic gate that is *reversible* (no information is lost)
and *universal* (all reversible logic circuits can be built using Toffoli gates).
It takes three input bits $A$, $B$ and $C$,
of which it returns $A$ and $B$ unchanged,
and flips $C$ if both $A$ and $B$ are true.
In circuit diagrams, its representation is:
 This gate is reversible, because $A$ and $B$ are preserved,
and are all you need to reconstruct to $C$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
This gate is reversible, because $A$ and $B$ are preserved,
and are all you need to reconstruct to $C$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
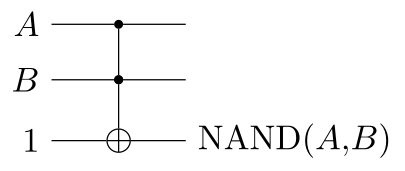 A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:
A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:
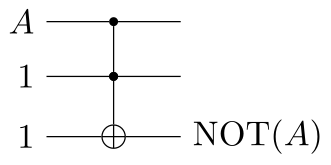
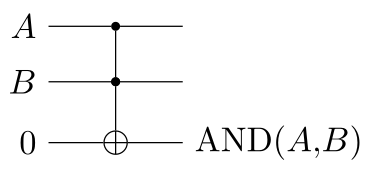
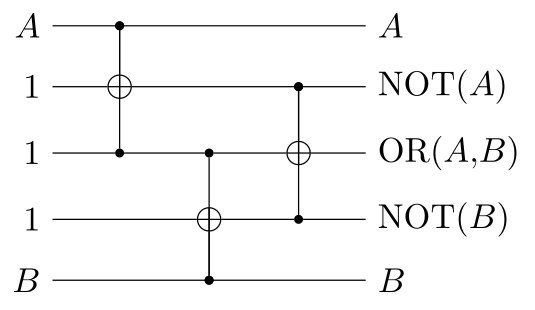
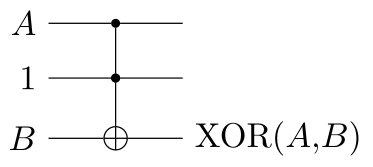 Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $A \lor B = \neg (\neg A \land \neg B)$,
i.e. OR is NAND of NOT $A$ and NOT $B$:
Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $A \lor B = \neg (\neg A \land \neg B)$,
i.e. OR is NAND of NOT $A$ and NOT $B$:
 Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $\ket{A} \ket{B} \ket{C}$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $\ket{\psi}$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \ket{100} + c_{101} \ket{101} + c_{110} \ket{110} + c_{111} \ket{111} \big)
\\
&= c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\quad\,\, c_{100} \ket{100} + c_{101} \ket{101} + c_{111} \ket{110} + c_{110} \ket{111}
\end{aligned}$$
Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $\ket{A} \ket{B} \ket{C}$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $\ket{\psi}$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \ket{100} + c_{101} \ket{101} + c_{110} \ket{110} + c_{111} \ket{111} \big)
\\
&= c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\quad\,\, c_{100} \ket{100} + c_{101} \ket{101} + c_{111} \ket{110} + c_{110} \ket{111}
\end{aligned}$$
 This gate is reversible, because $A$ and $B$ are preserved,
and are all you need to reconstruct to $C$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
This gate is reversible, because $A$ and $B$ are preserved,
and are all you need to reconstruct to $C$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
 A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:
A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:

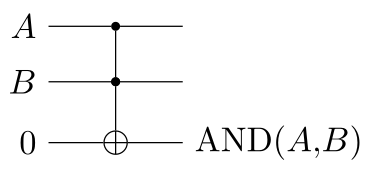
 Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $A \lor B = \neg (\neg A \land \neg B)$,
i.e. OR is NAND of NOT $A$ and NOT $B$:
Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $A \lor B = \neg (\neg A \land \neg B)$,
i.e. OR is NAND of NOT $A$ and NOT $B$:
 Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $\ket{A} \ket{B} \ket{C}$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $\ket{\psi}$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \ket{100} + c_{101} \ket{101} + c_{110} \ket{110} + c_{111} \ket{111} \big)
\\
&= c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\quad\,\, c_{100} \ket{100} + c_{101} \ket{101} + c_{111} \ket{110} + c_{110} \ket{111}
\end{aligned}$$
Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $\ket{A} \ket{B} \ket{C}$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $\ket{\psi}$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \ket{100} + c_{101} \ket{101} + c_{110} \ket{110} + c_{111} \ket{111} \big)
\\
&= c_{000} \ket{000} + c_{001} \ket{001} + c_{010} \ket{010} + c_{011} \ket{011} \\
&\quad\,\, c_{100} \ket{100} + c_{101} \ket{101} + c_{111} \ket{110} + c_{110} \ket{111}
\end{aligned}$$