---
title: "Quantum gate"
sort_title: "Quantum gate"
date: 2021-03-29
categories:
- Quantum information
layout: "concept"
---
In quantum computing, **quantum gates** are the equivalent
of classical binary logic gates such as $$\mathrm{NOT}$$, $$\mathrm{AND}$$, etc.
Because of the continuous nature of qubits,
the number of possible quantum gates is uncountably infinite,
so we only consider the most important examples here.
## One-qubit gates
As an example, consider the following must general single-qubit state $$\Ket{\psi}$$:
$$\begin{aligned}
\Ket{\psi}
= \alpha \Ket{0} + \beta \Ket{1}
= \begin{bmatrix} \alpha \\ \beta \end{bmatrix}
\end{aligned}$$
Arguably the most famous and/or most fundamental quantum gates are the **Pauli matrices**:
$$\begin{aligned}
\boxed{
X =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
}
\qquad
\boxed{
Y =
\begin{bmatrix}
0 & -i \\
i & 0
\end{bmatrix}
}
\qquad
\boxed{
Z =
\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}
}
\end{aligned}$$
They have the following effect on $$\Ket{\psi}$$.
Note that $$X$$ is equivalent to the classical $$\mathrm{NOT}$$ gate
(and is often given that name),
and $$Z$$ is sometimes called the **phase-flip gate**:
$$\begin{aligned}
X \Ket{\psi}
= \begin{bmatrix} \beta \\ \alpha \end{bmatrix}
\qquad
Y \Ket{\psi}
= \begin{bmatrix} -i \beta \\ i \alpha \end{bmatrix}
\qquad
Z \Ket{\psi}
= \begin{bmatrix} \alpha \\ -\beta \end{bmatrix}
\end{aligned}$$
In fact, $$Z$$ is a specific case of the **phase shift gate** $$R_\phi$$,
which modifies the qubit's phase without changing its amplitudes.
For an angle $$\phi$$, it is given by:
$$\begin{aligned}
\boxed{
R_\phi =
\begin{bmatrix}
1 & 0 \\
0 & e^{i \phi}
\end{bmatrix}
}
\end{aligned}$$
For $$\phi = \pi$$, we recover the Pauli-$$Z$$ gate.
In general, the action of $$R_\phi$$ is as follows:
$$\begin{aligned}
R_\phi \Ket{\psi}
= \begin{bmatrix} \alpha \\ e^{i \phi} \beta \end{bmatrix}
\end{aligned}$$
Two common special cases of $$R_\phi$$
are $$\phi = \pi/2$$ and $$\phi = \pi/4$$,
respectively called $$S$$ and $$T$$:
$$\begin{aligned}
\boxed{
S = R_{\pi/2} =
\begin{bmatrix}
1 & 0 \\
0 & i
\end{bmatrix}
}
\qquad \quad
\boxed{
T = R_{\pi/4} =
\frac{1}{\sqrt{2}}
\begin{bmatrix}
\sqrt{2} & 0 \\
0 & 1 + i
\end{bmatrix}
}
\end{aligned}$$
Finally, we have the **Hadamard gate** $$H$$,
which is defined as follows:
$$\begin{aligned}
\boxed{
H = \frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
}
\end{aligned}$$
Its action consists of rotating the qubit
by $$\pi$$ around the axis $$(X + Z) / \sqrt{2}$$ of the Bloch sphere:
$$\begin{aligned}
H \Ket{\psi}
= \frac{1}{\sqrt{2}} \begin{bmatrix} \alpha + \beta \\ \alpha - \beta \end{bmatrix}
\end{aligned}$$
Notably, it maps the eigenstates of $$X$$ and $$Z$$ to each other,
and is its own inverse (i.e. unitary):
$$\begin{aligned}
H \Ket{0} = \Ket{+}
\qquad
H \Ket{1} = \Ket{-}
\qquad
H \Ket{+} = \Ket{0}
\qquad
H \Ket{-} = \Ket{1}
\end{aligned}$$
The **Clifford gates** are a set including $$X$$, $$Y$$, $$Z$$, $$H$$ and $$S$$,
or more generally any gates that rotate
by multiples of $$\pi/2$$ around the Bloch sphere.
This set is **not universal**, meaning that if we start from $$\Ket{0}$$,
we can only reach $$\Ket{0}$$, $$\Ket{1}$$, $$\Ket{+}$$, $$\Ket{-}$$, $$\Ket{+i}$$ $$\Ket{-i}$$ using these gates.
If we add *any* non-Clifford gate, for example $$T$$,
then we can reach any point on the Bloch sphere,
which means that the set is **universal**.
However, there is a problem: a qubit has an uncountable infinity of states,
but a quantum circuit consists of a countably infinite sequence of gates, at most.
Therefore, technically, we can never reach the whole Bloch sphere,
but we *can* come up with circuits that approximate a target state to some degree $$\varepsilon$$.
This is the definition of universality:
any state can be approximated.
## Two-qubit gates
As an example, let us consider
the following two pure one-qubit states $$\Ket{\psi_1}$$ and $$\Ket{\psi_2}$$:
$$\begin{aligned}
\Ket{\psi_1}
= \alpha_1 \Ket{0} + \beta_1 \Ket{1}
= \begin{bmatrix} \alpha_1 \\ \beta_1 \end{bmatrix}
\qquad \quad
\Ket{\psi_2}
= \alpha_2 \Ket{0} + \beta_2 \Ket{1}
= \begin{bmatrix} \alpha_2 \\ \beta_2 \end{bmatrix}
\end{aligned}$$
The composite state of both qubits, assuming they are pure,
is then their tensor product $$\otimes$$:
$$\begin{aligned}
\Ket{\psi_1 \psi_2}
= \Ket{\psi_1} \otimes \Ket{\psi_2}
&= \alpha_1 \alpha_2 \Ket{00} + \alpha_1 \beta_2 \Ket{01} + \beta_1 \alpha_2 \Ket{10} + \beta_1 \beta_2 \Ket{11}
\\
&= c_{00} \Ket{00} + c_{01} \Ket{01} + c_{10} \Ket{10} + c_{11} \Ket{11}
\end{aligned}$$
Note that a two-qubit system may be [entangled](/know/concept/quantum-entanglement/),
in which case the coefficients $$c_{00}$$ etc. cannot be written as products,
i.e. $$\Ket{\psi_2}$$ cannot be expressed separately from $$\Ket{\psi_1}$$, and vice versa.
In other words, the general action of a two-qubit quantum gate
can be expressed in the basis of $$\Ket{00}$$, $$\Ket{01}$$, $$\Ket{10}$$ and $$\Ket{11}$$,
but not always in the basis of $$\Ket{0}_1$$, $$\Ket{1}_1$$, $$\Ket{0}_2$$ and $$\Ket{1}_2$$.
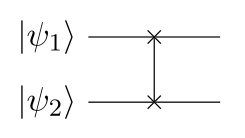
With that said, the first two-qubit gate is $$\mathrm{SWAP}$$,
which simply swaps $$\Ket{\psi_1}$$ and $$\Ket{\psi_2}$$:
 $$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $$\Ket{00}$$, $$\Ket{01}$$, $$\Ket{10}$$ and $$\Ket{11}$$.
Note that $$\mathrm{SWAP}$$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{10} \Ket{01} + c_{01} \Ket{10} + c_{11} \Ket{11}
\end{aligned}$$
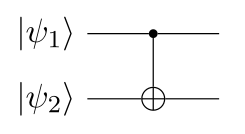
Next, there is the **controlled NOT gate** $$\mathrm{CNOT}$$,
which "flips" (applies $$X$$ to) $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
$$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $$\Ket{00}$$, $$\Ket{01}$$, $$\Ket{10}$$ and $$\Ket{11}$$.
Note that $$\mathrm{SWAP}$$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{10} \Ket{01} + c_{01} \Ket{10} + c_{11} \Ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $$\mathrm{CNOT}$$,
which "flips" (applies $$X$$ to) $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
 $$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $$c_{10}$$ and $$c_{11}$$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + c_{11} \Ket{10} + c_{10} \Ket{11}
\end{aligned}$$
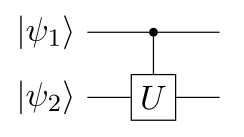
More generally, from every one-qubit gate $$U$$,
we can define a two-qubit **controlled U gate** $$\mathrm{CU}$$,
which applies $$U$$ to $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
$$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $$c_{10}$$ and $$c_{11}$$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + c_{11} \Ket{10} + c_{10} \Ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $$U$$,
we can define a two-qubit **controlled U gate** $$\mathrm{CU}$$,
which applies $$U$$ to $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
 $$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $$U$$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \Ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \Ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $$n$$ to $$n$$ qubits can be approximated using only these gates.
A minimal universal set is $$\{\mathrm{CNOT}, T, S\}$$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
$$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $$U$$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \Ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \Ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $$n$$ to $$n$$ qubits can be approximated using only these gates.
A minimal universal set is $$\{\mathrm{CNOT}, T, S\}$$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
 $$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $$\Ket{00}$$, $$\Ket{01}$$, $$\Ket{10}$$ and $$\Ket{11}$$.
Note that $$\mathrm{SWAP}$$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{10} \Ket{01} + c_{01} \Ket{10} + c_{11} \Ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $$\mathrm{CNOT}$$,
which "flips" (applies $$X$$ to) $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
$$\begin{aligned}
\boxed{
\mathrm{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\end{aligned}$$
This matrix is given in the basis of $$\Ket{00}$$, $$\Ket{01}$$, $$\Ket{10}$$ and $$\Ket{11}$$.
Note that $$\mathrm{SWAP}$$ cannot generate entanglement,
so if its input is separable, its output is too.
In any case, its effect is clear:
$$\begin{aligned}
\mathrm{SWAP} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{10} \Ket{01} + c_{01} \Ket{10} + c_{11} \Ket{11}
\end{aligned}$$
Next, there is the **controlled NOT gate** $$\mathrm{CNOT}$$,
which "flips" (applies $$X$$ to) $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
 $$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $$c_{10}$$ and $$c_{11}$$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + c_{11} \Ket{10} + c_{10} \Ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $$U$$,
we can define a two-qubit **controlled U gate** $$\mathrm{CU}$$,
which applies $$U$$ to $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
$$\begin{aligned}
\boxed{
\mathrm{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
That is, it swaps the last two coefficients $$c_{10}$$ and $$c_{11}$$ in the composite state vector:
$$\begin{aligned}
\mathrm{CNOT} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + c_{11} \Ket{10} + c_{10} \Ket{11}
\end{aligned}$$
More generally, from every one-qubit gate $$U$$,
we can define a two-qubit **controlled U gate** $$\mathrm{CU}$$,
which applies $$U$$ to $$\Ket{\psi_2}$$ if $$\Ket{\psi_1}$$ is true:
 $$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $$U$$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \Ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \Ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $$n$$ to $$n$$ qubits can be approximated using only these gates.
A minimal universal set is $$\{\mathrm{CNOT}, T, S\}$$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.
$$\begin{aligned}
\boxed{
\mathrm{CU} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}
\end{bmatrix}
}
\end{aligned}$$
Where the lower-right 2x2 block is simply $$U$$.
The general action of this gate is given by:
$$\begin{aligned}
\mathrm{CU} \Ket{\psi_1 \psi_2}
&= c_{00} \Ket{00} + c_{01} \Ket{01} + (c_{10} u_{00} + c_{11} u_{01}) \Ket{10} + (c_{10} u_{10} + c_{11} u_{11}) \Ket{11}
\end{aligned}$$
A set of gates is **universal** if all possible mappings
from $$n$$ to $$n$$ qubits can be approximated using only these gates.
A minimal universal set is $$\{\mathrm{CNOT}, T, S\}$$,
and there exist many others.
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
2. S. Aaronson,
*Introduction to quantum information science: lecture notes*,
2018, unpublished.