---
title: "Toffoli gate"
sort_title: "Toffoli gate"
date: 2021-04-09
categories:
- Quantum information
layout: "concept"
---
The **Toffoli gate** or **controlled-controlled-NOT (CCNOT) gate**
is a logic gate that is *reversible* (no information is lost)
and *universal* (all reversible logic circuits can be built using Toffoli gates).
It takes three input bits $$A$$, $$B$$ and $$C$$,
of which it returns $$A$$ and $$B$$ unchanged,
and flips $$C$$ if both $$A$$ and $$B$$ are true.
In circuit diagrams, its representation is:
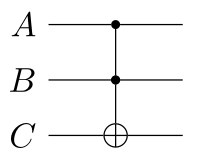 This gate is reversible, because $$A$$ and $$B$$ are preserved,
and are all you need to reconstruct to $$C$$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
This gate is reversible, because $$A$$ and $$B$$ are preserved,
and are all you need to reconstruct to $$C$$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
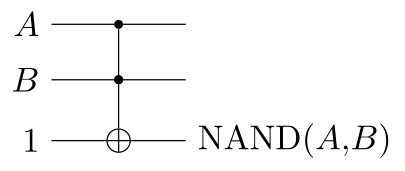 A NAND is enough to implement every conceivable circuit.
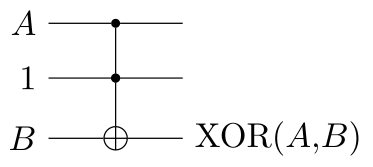
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:
A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:
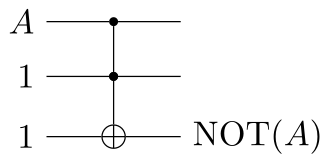
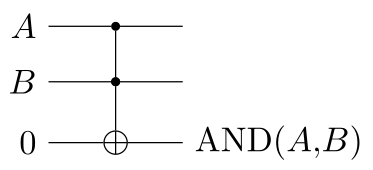
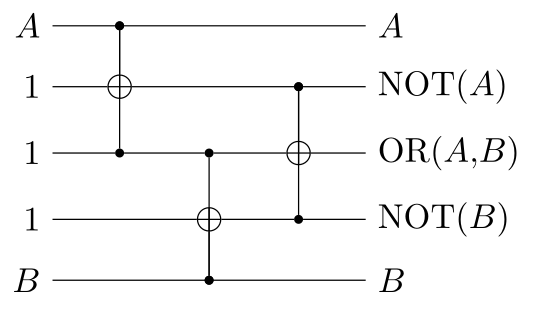
 Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $$A \lor B = \neg (\neg A \land \neg B)$$,
i.e. OR is NAND of NOT $$A$$ and NOT $$B$$:
Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $$A \lor B = \neg (\neg A \land \neg B)$$,
i.e. OR is NAND of NOT $$A$$ and NOT $$B$$:
 Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $$\Ket{A} \Ket{B} \Ket{C}$$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $$\Ket{\psi}$$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \Ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \Ket{100} + c_{101} \Ket{101} + c_{110} \Ket{110} + c_{111} \Ket{111} \big)
\\
&= c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\quad\,\, c_{100} \Ket{100} + c_{101} \Ket{101} + c_{111} \Ket{110} + c_{110} \Ket{111}
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $$\Ket{A} \Ket{B} \Ket{C}$$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $$\Ket{\psi}$$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \Ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \Ket{100} + c_{101} \Ket{101} + c_{110} \Ket{110} + c_{111} \Ket{111} \big)
\\
&= c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\quad\,\, c_{100} \Ket{100} + c_{101} \Ket{101} + c_{111} \Ket{110} + c_{110} \Ket{111}
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
 This gate is reversible, because $$A$$ and $$B$$ are preserved,
and are all you need to reconstruct to $$C$$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
This gate is reversible, because $$A$$ and $$B$$ are preserved,
and are all you need to reconstruct to $$C$$.
Moreover, this gate is universal,
because we can make a NAND gate from it:
 A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:
A NAND is enough to implement every conceivable circuit.
That said, we can efficiently implement NOT, AND, and XOR using a single Toffoli gate too.
Note that NOT is a special case of NAND:

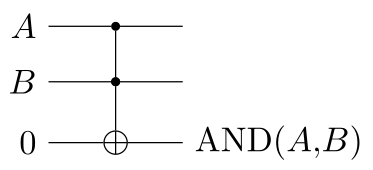
 Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $$A \lor B = \neg (\neg A \land \neg B)$$,
i.e. OR is NAND of NOT $$A$$ and NOT $$B$$:
Using these, we can, as an example, make an OR gate
from three Toffoli gates,
thanks to the fact that $$A \lor B = \neg (\neg A \land \neg B)$$,
i.e. OR is NAND of NOT $$A$$ and NOT $$B$$:
 Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $$\Ket{A} \Ket{B} \Ket{C}$$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $$\Ket{\psi}$$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \Ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \Ket{100} + c_{101} \Ket{101} + c_{110} \Ket{110} + c_{111} \Ket{111} \big)
\\
&= c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\quad\,\, c_{100} \Ket{100} + c_{101} \Ket{101} + c_{111} \Ket{110} + c_{110} \Ket{111}
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.
Thanks to its reversibility and universality,
the Toffoli gate is interesting for quantum computing.
Its [quantum gate](/know/concept/quantum-gate/) form is often called **CCNOT**.
In the basis $$\Ket{A} \Ket{B} \Ket{C}$$, its matrix is:
$$\begin{aligned}
\boxed{
\mathrm{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
}
\end{aligned}$$
If we apply this gate to an arbitrary three-qubit state $$\Ket{\psi}$$,
it swaps the last two coefficients:
$$\begin{aligned}
\mathrm{CCNOT} \Ket{\psi}
&= \mathrm{CCNOT} \big( c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\qquad\qquad\quad\:\; c_{100} \Ket{100} + c_{101} \Ket{101} + c_{110} \Ket{110} + c_{111} \Ket{111} \big)
\\
&= c_{000} \Ket{000} + c_{001} \Ket{001} + c_{010} \Ket{010} + c_{011} \Ket{011} \\
&\quad\,\, c_{100} \Ket{100} + c_{101} \Ket{101} + c_{111} \Ket{110} + c_{110} \Ket{111}
\end{aligned}$$
## References
1. J.S. Neergaard-Nielsen,
*Quantum information: lectures notes*,
2021, unpublished.