Categories: Algorithms, Quantum information.

Bernstein-Vazirani algorithm

In quantum information, the Bernstein-Vazirani algorithm proves the supremacy of quantum computers over classical deterministic or probabilistic computers. It is extremely similar to the Deutsch-Jozsa algorithm, and even uses the same circuit.

It solves a very artificial problem: we are given a “black box” function f(x)f(x) that takes an NN-bit xx and returns a single bit, which we are promised is the lowest bit of the bitwise dot product of xx with an unknown NN-bit string ss:

f(x)≡s⋅x  mod 2=(s1x1+s2x2+ ... +sNxN)  mod 2\begin{aligned} f(x) \equiv s \cdot x \:\bmod 2 = (s_1 x_1 + s_2 x_2 + \:...\: + s_N x_N) \:\bmod 2 \end{aligned}

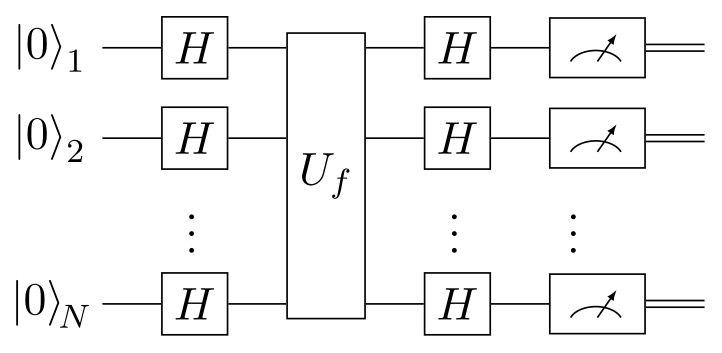
The goal is to find ss. To solve this problem, a classical computer would need to call f(x)f(x) exactly NN times with x=2nx = 2^n for n∈{0,...,N ⁣− ⁣1}n \in \{ 0, ..., N \!-\! 1\}. However, the Bernstein-Vazirani algorithm allows a quantum computer to do it with only a single query. It uses the following circuit:

Bernstein-Vazirani circuit

Where UfU_f is a phase oracle, whose action is defined as follows, where ∣x⟩=∣x1⟩⋯∣xN⟩\Ket{x} = \Ket{x_1} \cdots \Ket{x_N}:

∣x⟩→Uf→(−1)f(x)∣x⟩=(−1)s⋅x∣x⟩\begin{aligned} \Ket{x} \quad \to \boxed{U_f} \to \quad (-1)^{f(x)} \Ket{x} = (-1)^{s \cdot x} \Ket{x} \end{aligned}

That is, it introduces a phase flip based on the value of f(x)f(x). For an example implementation of such an oracle, see the Deutsch-Jozsa algorithm: its circuit is identical to this one, but describes UfU_f in a different (but equivalent) way.

Starting from the state ∣0⟩⊗N\Ket{0}^{\otimes N}, applying the Hadamard gate HH to all qubits yields:

∣0⟩⊗N→H⊗N→∣+⟩⊗N=12N∑x=02N−1∣x⟩\begin{aligned} \Ket{0}^{\otimes N} \quad \to \boxed{H^{\otimes N}} \to \quad \Ket{+}^{\otimes N} = \frac{1}{\sqrt{2^N}} \sum_{x = 0}^{2^N - 1} \Ket{x} \end{aligned}

This is an equal superposition of all candidates ∣x⟩\Ket{x}, which we feed to the oracle:

12N∑x=02N−1∣x⟩→Uf→12N∑x=02N−1(−1)s⋅x∣x⟩\begin{aligned} \frac{1}{\sqrt{2^N}} \sum_{x = 0}^{2^N - 1} \Ket{x} \quad \to \boxed{U_f} \to \quad \frac{1}{\sqrt{2^N}} \sum_{x = 0}^{2^N - 1} (-1)^{s \cdot x} \Ket{x} \end{aligned}

Then, using the definition of the Hadamard transform and the fact that it is its own inverse, one final set of HH-gates leads us to:

12N∑x=02N−1(−1)s⋅x∣x⟩→H⊗N→∣s⟩=∣s1⟩⋯∣sN⟩\begin{aligned} \frac{1}{\sqrt{2^N}} \sum_{x = 0}^{2^N - 1} (-1)^{s \cdot x} \Ket{x} \quad \to \boxed{H^{\otimes N}} \to \quad \Ket{s} = \Ket{s_1} \cdots \Ket{s_N} \end{aligned}

Which, upon measurement, gives us the desired binary representation of ss. For comparison, the Deutsch-Jozsa algorithm only cares whether s=0s = 0 or s≠0s \neq 0, whereas this algorithm is interested in the exact value of ss.

References

  1. J.S. Neergaard-Nielsen, Quantum information: lectures notes, 2021, unpublished.
  2. S. Aaronson, Introduction to quantum information science: lecture notes, 2018, unpublished.