---

Categories: Quantum information, Quantum mechanics, Two-level system.

Bloch sphere

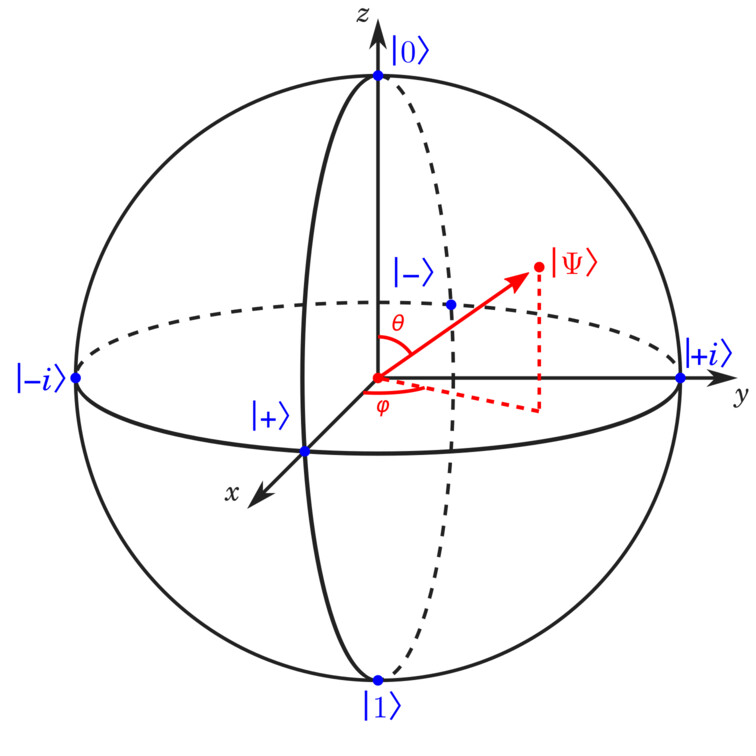
In quantum mechanics, particularly quantum information, the Bloch sphere is an invaluable tool to visualize qubits. All pure qubit states are represented by a point on the sphere’s surface:

The $x$, $y$ and $z$-axes represent the components of a spin-1/2-alike system, and their extremes are the eigenstates of the Pauli matrices:

$$\begin{aligned} \hat{\sigma}_z \to \{\ket{0}, \ket{1}\} \qquad \hat{\sigma}_x \to \{\ket{+}, \ket{-}\} \qquad \hat{\sigma}_y \to \{\ket{+i}, \ket{-i}\} \end{aligned}$$

Where the latter two pairs are expressed as follows in the conventional $z$-basis:

$$\begin{aligned} \ket{\pm} = \frac{\ket{0} \pm \ket{1}}{\sqrt{2}} \qquad \qquad \ket{\pm i} = \frac{\ket{0} \pm i \ket{1}}{\sqrt{2}} \end{aligned}$$

More generally, every point on the surface of the sphere describes a pure qubit state in terms of the angles $\theta$ and $\varphi$, respectively the elevation and azimuth:

$$\begin{aligned} \ket{\Psi} = \cos\!\Big(\frac{\theta}{2}\Big) \ket{0} + \exp(i \varphi) \sin\!\Big(\frac{\theta}{2}\Big) \ket{1} \end{aligned}$$

Another way to describe states is the Bloch vector $\vec{r}$, which is simply the $(x,y,z)$-coordinates of a point on the sphere. Let the radius $r \le 1$:

$$\begin{aligned} \boxed{ \vec{r} = \begin{bmatrix} r_x \\ r_y \\ r_z \end{bmatrix} = \begin{bmatrix} r \sin\theta \cos\varphi \\ r \sin\theta \sin\varphi \\ r \cos\theta \end{bmatrix} } \end{aligned}$$

Note that $\vec{r}$ is not actually a qubit state, but rather a description of one. The main point of the Bloch vector is that it allows us to describe the qubit using a density operator:

$$\begin{aligned} \boxed{ \hat{\rho} = \frac{1}{2} \Big( \hat{I} + \vec{r} \cdot \vec{\sigma} \Big) } \end{aligned}$$

Where $\vec{\sigma} = (\hat{\sigma}_x, \hat{\sigma}_y, \hat{\sigma}_z)$ is the Pauli “vector”. Now, we know that a density matrix represents a pure ensemble if and only if it is idempotent, i.e. $\hat{\rho}^2 = \hat{\rho}$:

$$\begin{aligned} \hat{\rho}^2 &= \frac{1}{4} \Big( \hat{I}^2 + 2 \hat{I} (\vec{r} \cdot \vec{\sigma}) + (\vec{r} \cdot \vec{\sigma})^2 \Big) = \frac{1}{4} \Big( \hat{I} + 2 (\vec{r} \cdot \vec{\sigma}) + (\vec{r} \cdot \vec{\sigma})^2 \Big) \end{aligned}$$

You can easily convince yourself that, if $(\vec{r} \cdot \vec{\sigma})^2 = \hat{I}$, we get $\hat{\rho}$ again, so the state is pure:

$$\begin{aligned} (\vec{r} \cdot \vec{\sigma})^2 &= (r_x \hat{\sigma}_x + r_y \hat{\sigma}_y + r_z \hat{\sigma}_z)^2 \\ &= r_x^2 \hat{\sigma}_x^2 + r_x r_y \hat{\sigma}_x \hat{\sigma}_y + r_x r_z \hat{\sigma}_x \hat{\sigma}_z + r_x r_y \hat{\sigma}_y \hat{\sigma}_x + r_y^2 \hat{\sigma}_y^2 \\ &\quad + r_y r_z \hat{\sigma}_y \hat{\sigma}_z + r_x r_z \hat{\sigma}_z \hat{\sigma}_x + r_y r_z \hat{\sigma}_z \hat{\sigma}_y + r_z^2 \hat{\sigma}_z^2 \\ &= r_x^2 \hat{I} + r_y^2 \hat{I} + r_z^2 \hat{I} + r_x r_y \{ \hat{\sigma}_x, \hat{\sigma}_y \} + r_y r_z \{ \hat{\sigma}_y, \hat{\sigma}_z \} + r_x r_z \{ \hat{\sigma}_x, \hat{\sigma}_z \} \\ &= (r_x^2 + r_y^2 + r_z^2) \hat{I} = r^2 \hat{I} \end{aligned}$$

Therefore, if the radius $r = 1$, the ensemble is pure, else if $r < 1$ it is mixed.

Another useful property of the Bloch vector is that the expectation value of the Pauli matrices are given by the corresponding component of $\vec{r}$:

$$\begin{aligned} \boxed{ \begin{aligned} \expval{\hat{\sigma}_{x}} &= r_{x} \\ \expval{\hat{\sigma}_{y}} &= r_{y} \\ \expval{\hat{\sigma}_{z}} &= r_{z} \end{aligned} } \end{aligned}$$

This is a consequence of the above form of the density operator $\hat{\rho}$. For example for $\hat{\sigma}_z$:

$$\begin{aligned} \expval{\hat{\sigma}_z} &= \Tr(\hat{\rho} \hat{\sigma}_z) = \frac{1}{2} \Tr\!\big(\hat{\sigma}_z + (\vec{r} \cdot \vec{\sigma}) \hat{\sigma}_z \big) = \frac{1}{2} \Tr\!\big( (r_x \hat{\sigma}_x + r_y \hat{\sigma}_y + r_z \hat{\sigma}_z) \hat{\sigma}_z \big) \\ &= \frac{1}{2} \Tr\!\big( r_x \hat{\sigma}_x \hat{\sigma}_z + r_y \hat{\sigma}_y \hat{\sigma}_z + r_z \hat{\sigma}_z^2 \big) = \frac{1}{2} \Tr\!\big( r_z \hat{I} \big) = r_z \end{aligned}$$

References

1. N. Brunner, Quantum information theory: lecture notes, 2019, unpublished.
2. J.B. Brask, Quantum information: lecture notes, 2021, unpublished.

---