---

Categories: Fluid mechanics, Physics.

Metacentric height

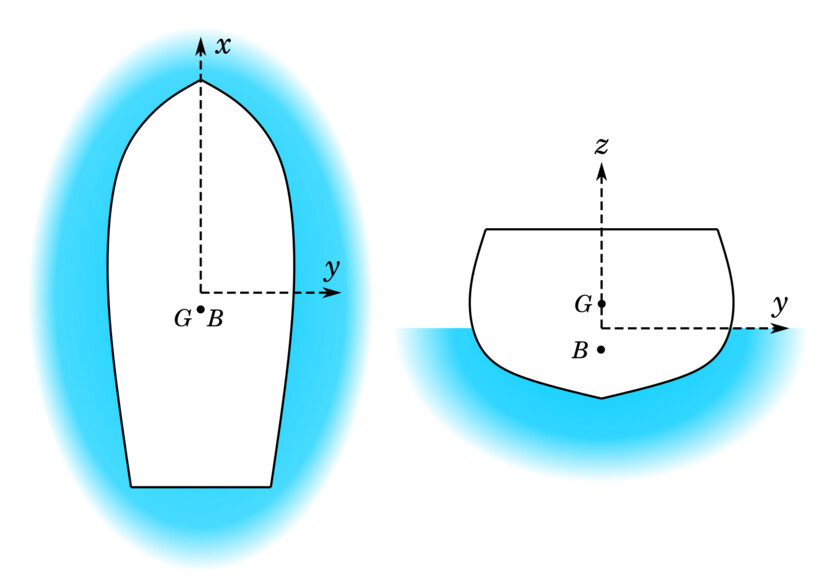
Consider an object with center of mass $G$, floating in a large body of liquid whose surface is flat at $z = 0$. For our purposes, it is easiest to use a coordinate system whose origin is at the area centroid of the object’s cross-section through the liquid’s surface, namely:

$$\begin{aligned} (x_0, y_0) \equiv \frac{1}{A_{wl}} \iint_{wl} (x, y) \dd{A} \end{aligned}$$

Where $A_{wl}$ is the cross-sectional area enclosed by the “waterline” around the “boat”. Note that the boat’s center of mass $G$ does not coincide with the origin in general, as is illustrated in the following sketch of our choice of coordinate system:

Here, $B$ is the center of buoyancy, equal to the center of mass of the volume of water displaced by the boat as per Archimedes’ principle. At equilibrium, the forces of buoyancy $\vb{F}_B$ and gravity $\vb{F}_G$ have equal magnitudes in opposite directions, and $B$ is directly above or below $G$, or in other words, $x_B = x_G$ and $y_B = y_G$, which are calculated as follows:

$$\begin{aligned} (x_G, y_G, z_G) &\equiv \frac{1}{V_{boat}} \iiint_{boat} (x, y, z) \dd{V} \\ (x_B, y_B, z_B) &\equiv \frac{1}{V_{disp}} \iiint_{disp} (x, y, z) \dd{V} \end{aligned}$$

Where $V_{boat}$ is the volume of the whole boat, and $V_{disp}$ is the volume of liquid it displaces.

Whether a given equilibrium is stable is more complicated. Suppose the ship is tilted by a small angle $\theta$ around the $x$-axis, in which case the old waterline, previously in the $z = 0$ plane, gets shifted to a new plane, namely:

$$\begin{aligned} z = \sin(\theta) \: y \approx \theta y \end{aligned}$$

Then $V_{disp}$ changes by $\Delta V_{disp}$, which is estimated below. If a point of the old waterline is raised by $z$, then the displaced liquid underneath it is reduced proportionally, hence the sign:

$$\begin{aligned} \Delta V_{disp} \approx - \iint_{wl} z \dd{A} \approx - \theta \iint_{wl} y \dd{A} = 0 \end{aligned}$$

So $V_{disp}$ is unchanged, at least to first order in $\theta$. However, the shape of the displaced volume may have changed significantly. Therefore, the shift of the position of the buoyancy center from $B$ to $B'$ involves a correction $\Delta y_B$ in addition to the rotation by $\theta$:

$$\begin{aligned} y_B' = y_B - \theta z_B + \Delta y_B \end{aligned}$$

We find $\Delta y_B$ by calculating the virtual buoyancy center of the shape difference: on the side of the boat that has been lifted by the rotation, the center of buoyancy is “pushed” away due to the reduced displacement there, and vice versa on the other side. Consequently:

$$\begin{aligned} \Delta y_B = - \frac{1}{V_{disp}} \iint_{wl} y z \dd{A} \approx - \frac{\theta}{V_{disp}} \iint_{wl} y^2 \dd{A} = - \frac{\theta I}{V_{disp}} \end{aligned}$$

Where we have defined the so-called area moment $I$ of the waterline as follows:

$$\begin{aligned} \boxed{ I \equiv \iint_{wl} y^2 \dd{A} } \end{aligned}$$

Now that we have an expression for $\Delta y_B$, the new center’s position $y_B'$ is found to be:

$$\begin{aligned} y_B' = y_B - \theta \Big( z_B + \frac{I}{V_{disp}} \Big) \approx y_B - \sin(\theta) \: \Big( z_B + \frac{I}{V_{disp}} \Big) \end{aligned}$$

This looks like a rotation by $\theta$ around a so-called metacenter $M$, with a height $z_M$ known as the metacentric height, defined as:

$$\begin{aligned} \boxed{ z_M \equiv z_B + \frac{I}{V_{disp}} } \end{aligned}$$

Meanwhile, the position of $M$ is defined such that it lies on the line between the old centers $G$ and $B$. Our calculation of $y_B'$ has shown that the new $B'$ always lies below $M$.

After the rotation, the boat is not in equilibrium anymore, because the new $G'$ is not directly above or below $B'$. The force of gravity then causes a torque $\vb{T}$ given by:

$$\begin{aligned} \vb{T} = (\vb{r}_G' - \vb{r}_B') \cross m \vb{g} \end{aligned}$$

Where $\vb{g}$ points downwards. Since the rotation was around the $x$-axis, we are only interested in the $x$-component $T_x$, which becomes:

$$\begin{aligned} T_x = - (y_G' - y_B') m \mathrm{g} = - \big((y_G - \theta z_G) - (y_B - \theta z_M)\big) m \mathrm{g} \end{aligned}$$

With $y_G' = y_G - \theta z_G$ being a simple rotation of $G$. At the initial equilibrium $y_G = y_B$, so:

$$\begin{aligned} T_x = \theta (z_G - z_M) m \mathrm{g} \end{aligned}$$

If $z_M < z_G$, then $T_x$ has the same sign as $\theta$, so $\vb{T}$ further destabilizes the boat. But if $z_M > z_G$, then $\vb{T}$ counteracts the rotation, and the boat returns to the original equilibrium, leading us to the following stability condition:

$$\begin{aligned} \boxed{ z_M > z_G } \end{aligned}$$

In other words, for a given boat design (or general shape) $z_G$ and $z_M$ can be calculated, and as long as they satisfy the above inequality, it will float stably in water (or any other fluid, although the buoyancy depends significantly on the density).

References

1. B. Lautrup, Physics of continuous matter: exotic and everyday phenomena in the macroscopic world, 2nd edition, CRC Press.

---