---

Categories: Algorithms, Cryptography, Quantum information.

Shor’s algorithm

Shor’s algorithm was the first truly useful quantum algorithm. It can solve important problems, most notably integer factorization, much more efficiently than any classical algorithm. It weakens widely-used cryptographic schemes, such as RSA and Diffie-Hellman.

In essence, Shor’s algorithm’s revolutionary achievement is that it can efficiently find the periods $s_1, ..., s_A$ of a function $f(x_1, ..., x_A)$ on a discrete finite field, where:

$$\begin{aligned} f(x_1, ..., x_A) = f(x_1 + s_1, ..., x_A + s_A) \end{aligned}$$

This is a so-called hidden subgroup problem for a finite Abelian group. With minimal modifications, Shor’s algorithm can solve practically every such problem.

Integer factorization

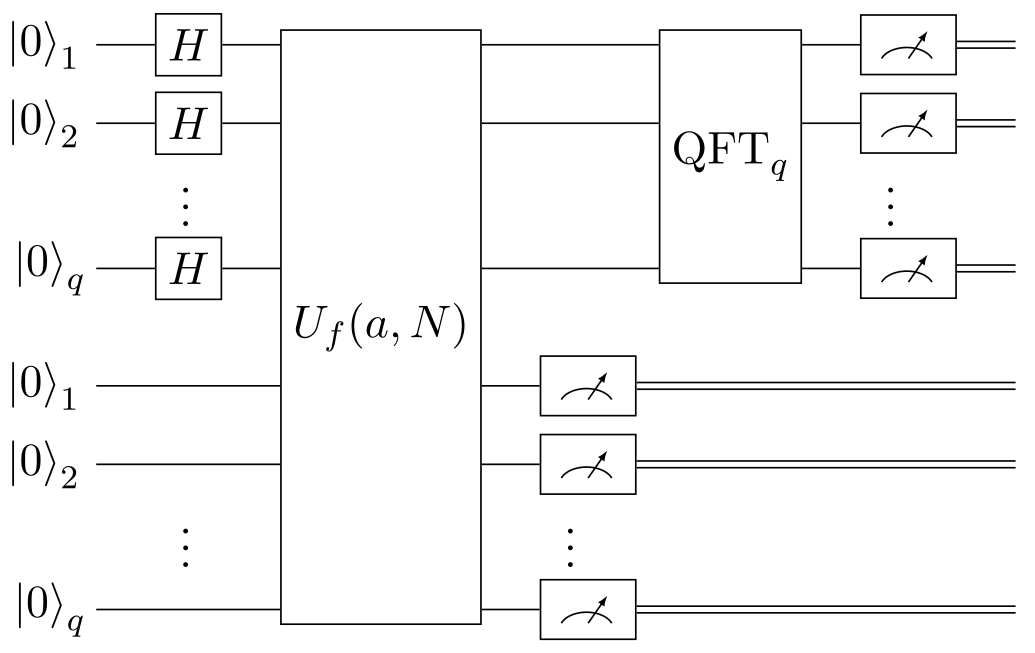
Originally, Shor’s algorithm was designed to factorize an integer $N$. For reasons explained later, this means our goal is to find the period $s$ of the modular exponentiation function $f$:

$$\begin{aligned} f(x) = a^x \bmod N \end{aligned}$$

For a given $a$ and $N$. The period $s$ is the smallest integer satisfying $f(x) = f(x+s)$. To do this, the following $2q$-qubit quantum circuit is used, with $q$ chosen so that $N^2 \le 2^q < 2 N^2$:

Here, $\mathrm{QFT}_q$ refers to the $q$-qubit quantum Fourier transform, and the oracle $U_f$ calculates $f(x)$ for predetermined values of $a$ and $N$. It is an XOR oracle, working as follows:

$$\begin{aligned} \Ket{x} \Ket{y} \quad \to \boxed{U_f(a, N)} \to \quad \Ket{x} \Ket{y \oplus f(x)} \end{aligned}$$

Execution starts by applying the Hadamard gate $H$ to the first $q$ qubits, yielding:

$$\begin{aligned} \Ket{0}^{\otimes q} \Ket{0}^{\otimes q} \quad \to \boxed{H^{\otimes q}} \to \quad \Ket{+}^{\otimes q} \Ket{0}^{\otimes q} = \frac{1}{\sqrt{Q}} \sum_{x = 0}^{Q - 1} \Ket{x} \Ket{0}^{\otimes q} \end{aligned}$$

Where $Q = 2^q$, and $\Ket{x}$ is the computational basis state $\Ket{x_1} \cdots \Ket{x_q}$. Moving on to $U_f$:

$$\begin{aligned} \frac{1}{\sqrt{Q}} \sum_{x = 0}^{Q - 1} \Ket{x} \Ket{0}^{\otimes q} \quad \to \boxed{U_f(a, N)} \to \quad \frac{1}{\sqrt{Q}} \sum_{x = 0}^{Q - 1} \Ket{x} \Ket{f(x)} \end{aligned}$$

Then we measure $f(x)$, causing it collapse as follows for an unknown arbitrary value of $x_0$:

$$\begin{aligned} f(x_0) = f(x_0 + s) = f(x_0 + 2s) = \cdots = f(x_0 + (L-1) s) \end{aligned}$$

Due to entanglement, the unmeasured (top $q$) qubits change state into a superposition:

$$\begin{aligned} \frac{1}{\sqrt{L}} \sum_{\ell = 0}^{L - 1} \Ket{x_0 + \ell s} \end{aligned}$$

Clearly, there is a periodic structure here, but we cannot measure it directly, because we do not know the value of $x_0$, which, to make matters worse, changes every time we run the algorithm. This is where the QFT comes in, which outputs the following state:

$$\begin{aligned} \frac{1}{\sqrt{QL}} \sum_{k = 0}^{Q - 1} \bigg( \sum_{\ell = 0}^{L - 1} \omega_Q^{(x_0 + \ell s) k} \bigg) \Ket{k} \end{aligned}$$

Where $\omega_Q$ is a $Q$th root of unity. Measuring this state yields a $\Ket{k}$, with a probability $P(k)$:

$$\begin{aligned} P(k) = \frac{1}{QL} \bigg| \sum_{\ell = 0}^{L - 1} \omega_Q^{(x_0 + \ell s) k} \bigg|^2 = \frac{1}{QL} \bigg| \omega_Q^{x_0 k} \sum_{\ell = 0}^{L - 1} \omega_Q^{\ell s k} \bigg|^2 = \frac{1}{QL} \bigg| \sum_{\ell = 0}^{L - 1} \omega_Q^{\ell s k} \bigg|^2 \end{aligned}$$

The last step holds because $|\omega_Q| = 1$. Surprisingly, this implies that we did not need to perform the measurement of $f(x)$ earlier! This makes sense: the period $s$ does not depend on $x_0$, so why would we need an implicit $x_0$ to determine $s$?

So, what does the above probability $P(k)$ work out to? There are two cases:

$$\begin{alignedat}{2} &\mathrm{if} \: \omega_Q^{sk} = 1: \qquad &&P(k) = \frac{1}{QL} |L|^2 = \frac{L}{Q} \\ &\mathrm{if} \: \omega_Q^{sk} \neq 1: \qquad &&P(k) = \frac{1}{QL} \Bigg| \frac{1 - \omega_Q^{sk L}}{1 - \omega_Q^{sk}} \Bigg|^2 \end{alignedat}$$

Where the latter case was evaluated as a geometric series. The condition $\omega_Q^{sk}\!=\!1$ is equivalent to asking if $sk$ is a multiple of $Q$, i.e. if $sk = cQ$, for an integer $c$.

Recall that $L$ is the number of times that $s$ fits in $Q$, so $L\!=\!\lfloor Q / s \rfloor$. Assuming $Q/s$ is an integer, then $L\!=\!Q/s$ and $Q\!=\!s L$, which tells us that $\omega_Q^{sk}\!=\!\omega_{s L}^{s k}\!=\!\omega_L^k$. This implies that if $k$ is a multiple of $L$ (i.e. $k\!=\!c L$), then $\omega_L^k\!=\!1$, so $P(k) = L / Q$, which is exactly what we got earlier!

In other words, the condition $\omega_Q^{sk}\!=\!1$ is equivalent to $Q/s$ being an integer. In that case, we have that $Q\!=\!sL$, which we substitute into $P(k)$ from earlier:

$$\begin{aligned} \mathrm{if} \: (Q/s) \in \mathbb{N}: \qquad P(k) = \frac{L}{Q} = \frac{1}{s} \end{aligned}$$

And because $k$ is a multiple of $L$, and $L$ fits $s$ times in $Q$, there must be exactly $s$ values of $k$ that satisfy $P(k) = 1/s$. Therefore the probability of all other $k$-values is zero! This becomes clearer when you look at the sum used to calculate $P(k)$: if $Q\!=\!sL$, then it sums $\omega_L^{\ell k}$ over $\ell$, leading to perfect destructive interference for the “bad” $k$-values, leaving only the “good” ones.

So, to summarize: if $Q/s$ is an integer, then measuring only yields $k$-values that are multiples of $L\!=\!Q/s$. Running Shor’s algorithm several times then gives several $k$-values separated by $L$. That tells us what $L$ is, and we already know $Q$, so we finally find the period $s = Q/L$.

That begs the question: what if $Q/s$ is not an integer? We cannot check this, since $s$ is unknown! Instead, we rewrite the probability $P(k)$ as follows:

$$\begin{aligned} \mathrm{if} \: (Q/s) \not\in \mathbb{N}: \qquad P(k) = \frac{1}{QL} \Bigg| \frac{1 - \omega_Q^{sk L}}{1 - \omega_Q^{sk}} \Bigg|^2 = \frac{1}{QL} \Bigg| \frac{\sin(\pi s k L / Q)}{\sin(\pi s k / Q)} \Bigg|^2 \end{aligned}$$

This function peaks if $s k$ is close to a multiple of $Q$, i.e. $s k \approx c Q$, which we rearrange:

$$\begin{aligned} \frac{k}{Q} \approx \frac{c}{s} \end{aligned}$$

We know the left-hand side, and, from the definition of $f(x)$, clearly $s \le N$. We chose $Q \sim N^2$, so $s$ is quite small, and consequently $c$ is too, since $k < Q$.

In other words, $c/s$ is a “simple” fraction, so our goal is to find a “simple” fraction that is close to the “complicated” fraction $k/Q$. For example, if $k/Q\!=\!0.332$, then probably $c/s\!=\!1/3$.

This can be done rigorously using the continued fractions algorithm: write $k/Q$ as a continued fraction, until the non-integer part of the denominator becomes small enough. This part is then neglected, and we calculate whatever is left, to get an estimate of $c/s$.

Of course, $P(k)$ is a probability distribution, so even though the odds are in our favour, we might occasionally measure a misleading $k$-value. Running Shor’s algorithm several times “fixes” this.

So, to summarize: if $Q/s$ is not an integer, the measured $k$-values are generally close to $c Q / s$ for an integer $c$. By approximating $k/Q$ using the continued fraction algorithm, we estimate $c/s$. Repeating this procedure gives several values of $c/s$, such that $s$ is easy to deduce by taking the least common multiple of the denominators.

In any case, once we think we have $s$, we can easily verify that $f(x)\!=\!f(x\!+\!s)$. Whether $s$ is the smallest such integer depends on how lucky we are, but fortunately, for most applications of this algorithm, that does not actually matter, and usually we find the smallest $s$ anyway.

You typically need to repeat the algorithm $\mathcal{O}(\log{q})$ times, and the QFT is $\mathcal{O}(q^2)$. The bottleneck is modular exponentiation $f$, which is $\mathcal{O}(q^2 (\log{q}) \log{\log{q}})$ and therefore worse than the QFT, yielding a total complexity of $\mathcal{O}(q^2 (\log{q})^2 \log{\log{q}})$.

OK, but what does $s$ have to do with factorizing integers? Well, recall that $f$ is given by:

$$\begin{aligned} f(x) = a^x \bmod N \end{aligned}$$

$N$ is the number to factorize, and $a$ is a random integer coprime to $N$, meaning $\gcd(a, N) = 1$. The fact that $s$ is the period of $f$ for a certain $a$-value, implies that:

$$\begin{aligned} a^x = a^{x + s} \bmod N \quad \implies \quad 1 = a^s \bmod N \end{aligned}$$

Suppose that $s$ is even. In that case, we can rewrite the above equation as follows:

$$\begin{aligned} (a^{s/2})^2 - 1 = 0 \bmod N \end{aligned}$$

In other words, $(a^{s/2})^2 \!-\! 1$ is a multiple of $N$. We then use that $(a\!-\!b) (a\!+\!b) = a^2\!-\!b^2$:

$$\begin{aligned} \big( a^{s/2} - 1 \big) \big( a^{s/2} + 1 \big) = 0 \bmod N \end{aligned}$$

Because $s$ is even by assumption, the two factors on the left are integers, and as just mentioned, their product is a multiple of $N$. Then we only need to calculate:

$$\begin{aligned} \gcd\!\big( a^{s/2}\!-\!1, N \big) > 1 \quad\:\: \mathrm{and} \quad\:\: \gcd\!\big( a^{s/2}\!+\!1, N \big) > 1 \end{aligned}$$

And there we have the factors of $N$! The $\gcd$ can be calculated efficiently in $\mathcal{O}(q^2)$ time.

But what if $s$ is odd? No problem, then we just choose a new $a$ coprime to $N$, and keep repeating Shor’s algorithm until we do find an even $s$. We do the same if $a^{s/2}\!\pm\!1$ is itself a multiple of $N$.

References

1. J.S. Neergaard-Nielsen, Quantum information: lectures notes, 2021, unpublished.
2. S. Aaronson, Introduction to quantum information science: lecture notes, 2018, unpublished.

---