Categories: Fiber optics, Optics, Physics.

Dispersive broadening

In optical fibers, dispersive broadening is a linear effect where group velocity dispersion (GVD) “smears out” a pulse in the time domain due to the different group velocities of its frequencies, since pulses always have a nonzero width in the $\omega$ -domain. No new frequencies are created.

A pulse envelope $A(z, t)$ inside a fiber must obey the nonlinear Schrödinger equation, where the parameters $\beta_2$ and $\gamma$ respectively control dispersion and nonlinearity:

\begin{aligned} 0 = i \pdv{A}{z} - \frac{\beta_2}{2} \pdvn{2}{A}{t} + \gamma |A|^2 A \end{aligned}

We set $\gamma = 0$ to ignore all nonlinear effects, and consider a Gaussian initial condition:

\begin{aligned} A(0, t) = \sqrt{P_0} \exp\!\bigg(\!-\!\frac{t^2}{2 T_0^2}\bigg) \end{aligned}

By Fourier transforming in $t$ , the full analytical solution $A(z, t)$ is found to be as follows, where it can be seen that the amplitude decreases and the width increases with $z$ :

\begin{aligned} A(z,t) = \sqrt{\frac{P_0}{1 - i \beta_2 z / T_0^2}} \exp\!\bigg(\! -\!\frac{t^2 / (2 T_0^2)}{1 + \beta_2^2 z^2 / T_0^4} \big( 1 + i \beta_2 z / T_0^2 \big) \bigg) \end{aligned}

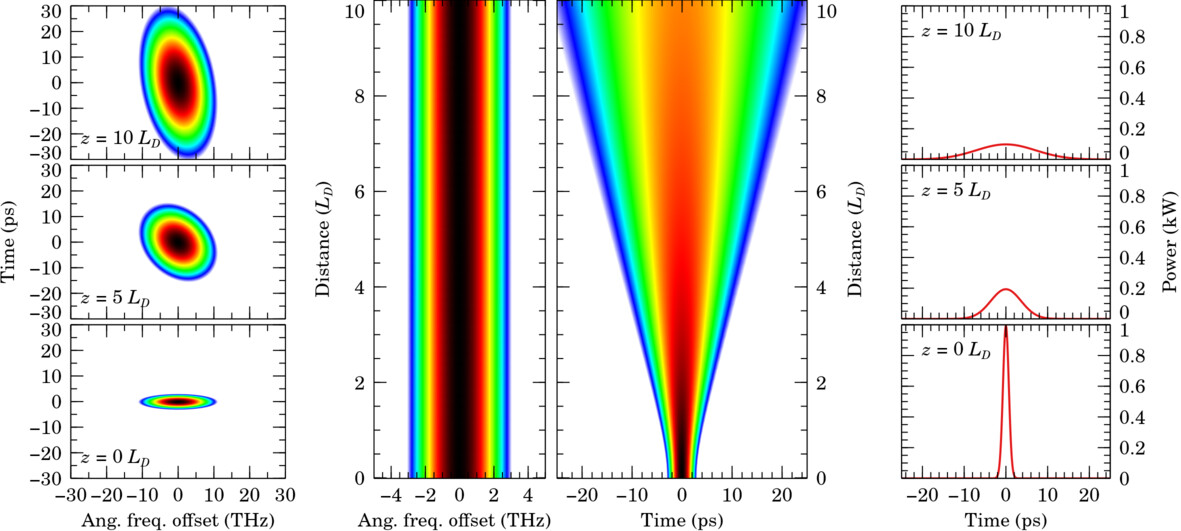
To quantify the strength of dispersive effects, we define the dispersion length $L_D$ as the distance over which the half-width at $1/e$ of maximum power (initially $T_0$ ) increases by a factor of $\sqrt{2}$ :

\begin{aligned} T_0 \sqrt{1 + \beta_2^2 L_D^2 / T_0^4} = T_0 \sqrt{2} \qquad \implies \qquad \boxed{ L_D \equiv \frac{T_0^2}{|\beta_2|} } \end{aligned}

This phenomenon is illustrated below for our example of a Gaussian pulse with parameter values $T_0 = 1\:\mathrm{ps}$ , $P_0 = 1\:\mathrm{kW}$ , $\beta_2 = -10 \:\mathrm{ps}^2/\mathrm{m}$ and $\gamma = 0$ :

The instantaneous frequency $\omega_\mathrm{GVD}(z, t)$ , which describes the dominant angular frequency at a given point in the time domain, is found to be as follows for the Gaussian pulse, where $\phi(z, t)$ is the phase of $A(z, t) = \sqrt{P(z, t)} \exp(i \phi(z, t))$ :

\begin{aligned} \omega_{\mathrm{GVD}}(z,t) = \pdv{}{t}\bigg( \frac{\beta_2 z t^2 / (2 T_0^4)}{1 + \beta_2^2 z^2 / T_0^4} \bigg) = \frac{\beta_2 z / T_0^2}{1 + \beta_2^2 z^2 / T_0^4} \frac{t}{T_0^2} \end{aligned}

This expression is linear in time, and depending on the sign of $\beta_2$ , frequencies on one side of the pulse arrive first, and those on the other side arrive last. The effect is stronger for smaller $T_0$ : this makes sense, since shorter pulses are spectrally wider.

The interaction between dispersion and self-phase modulation leads to many interesting effects, such as modulational instability and optical wave breaking. Of great importance is the sign of $\beta_2$ : in the anomalous dispersion regime ( $\beta_2 < 0$ ), lower frequencies travel more slowly than higher ones, and vice versa in the normal dispersion regime ( $\beta_2 > 0$ ).

References

O. Bang, Numerical methods in photonics: lecture notes, 2019, unpublished.