Categories: Fiber optics, Nonlinear optics, Optics, Physics.

Self-phase modulation

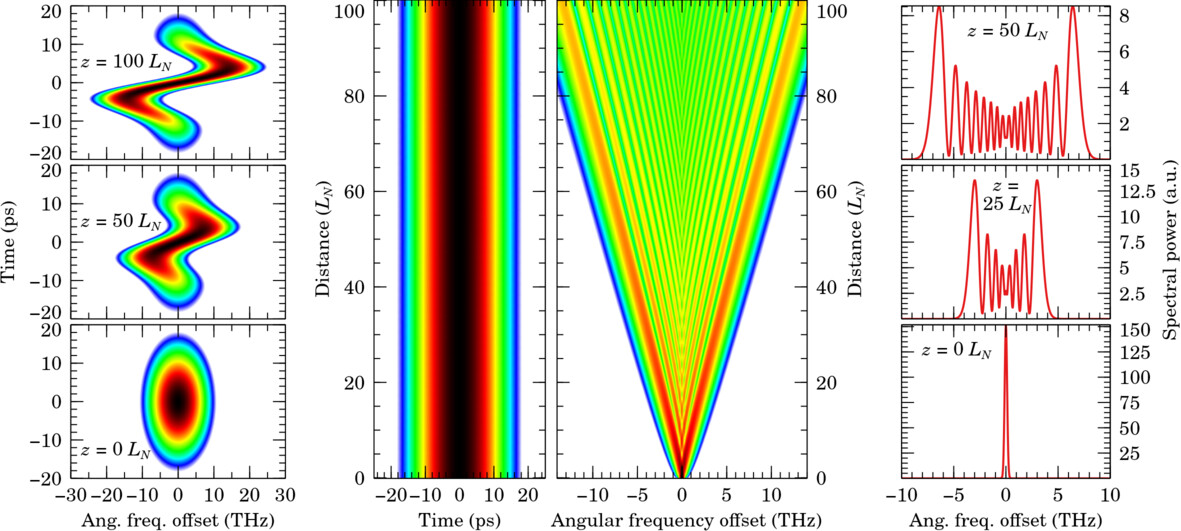
In fiber optics, self-phase modulation (SPM) is a nonlinear effect that gradually broadens pulses’ spectra. Unlike dispersion, SPM creates frequencies: in the $\omega$ -domain, the pulse steadily spreads out in a distinctive “accordion” shape. Lower frequencies are created at the front of the pulse and higher ones at the back, giving S-shaped spectrograms.

A pulse envelope $A(z, t)$ inside a fiber must obey the nonlinear Schrödinger equation, where the parameters $\beta_2$ and $\gamma$ respectively control dispersion and nonlinearity:

\begin{aligned} 0 = i \pdv{A}{z} - \frac{\beta_2}{2} \pdvn{2}{A}{t} + \gamma |A|^2 A \end{aligned}

By setting $\beta_2 = 0$ to neglect dispersion, solving this equation becomes trivial. For any arbitrary input pulse $A_0(t) = A(0, t)$ , we arrive at the following analytical solution:

\begin{aligned} A(z,t) = A_0 \exp\!\big( i \gamma |A_0|^2 z\big) \end{aligned}

The intensity $|A|^2$ in the time domain is thus unchanged, and only its phase is modified. Clearly, the largest phase shift increase occurs at the peak, where the intensity is $P_0$ . To quantify this, it is useful to define the nonlinear length $L_N$ , which gives the distance after which the phase of the peak has increased by exactly 1 radian:

\begin{aligned} \gamma P_0 L_N = 1 \qquad \implies \qquad \boxed{ L_N \equiv \frac{1}{\gamma P_0} } \end{aligned}

SPM is illustrated below for the following Gaussian initial pulse envelope, with parameter values $T_0 = 6\:\mathrm{ps}$ , $P_0 = 1\:\mathrm{kW}$ , $\beta_2 = 0$ , and $\gamma = 0.1/\mathrm{W}/\mathrm{m}$ :

\begin{aligned} A(0, t) = \sqrt{P_0} \exp\!\Big(\!-\!\frac{t^2}{2 T_0^2}\Big) \end{aligned}

From earlier, we then know the analytical solution for the $z$ -evolution:

\begin{aligned} A(z, t) = \sqrt{P_0} \exp\!\Big(\!-\!\frac{t^2}{2 T_0^2}\Big) \exp\!\bigg( i \gamma z P_0 \exp\!\Big(\!-\!\frac{t^2}{T_0^2}\Big) \bigg) \end{aligned}

The instantaneous frequency $\omega_\mathrm{SPM}(z, t)$ , which describes the dominant angular frequency at a given point in the time domain, is found to be as follows for the Gaussian pulse, where $\phi(z, t)$ is the phase of $A(z, t) = \sqrt{P(z, t)} \exp(i \phi(z, t))$ :

\begin{aligned} \omega_{\mathrm{SPM}}(z,t) = - \pdv{\phi}{t} = 2 \gamma z P_0 \frac{t}{T_0^2} \exp\!\Big(\!-\!\frac{t^2}{T_0^2}\Big) \end{aligned}

This result gives the S-shaped spectrograms seen in the illustration. The frequency shift thus not only depends on $L_N$ , but also on $T_0$ : the spectra of narrow pulses broaden much faster.

The interaction between self-phase modulation and dispersion leads to many interesting effects, such as modulational instability and optical wave breaking.

References

O. Bang, Numerical methods in photonics: lecture notes, 2019, unpublished.