---

Categories: Algorithms, Quantum information.

Simon’s algorithm

Simon’s algorithm was the first proof that quantum computers are able to solve some problems exponentially faster than classical computers. In the same spirit as the Deutsch-Jozsa algorithm and the Bernstein-Vazirani algorithm, the problem it solves, known as Simon’s problem, is of no practical use, but nevertheless Simon’s algorithm is an important milestone.

Simon’s problem is this: we are given a “black box” function $f(x)$ that takes an $n$-bit input $x$ and returns an $n$-bit output. We are promised that there exists an $s$ such that for all $x_1$ and $x_2$:

$$\begin{aligned} f(x_1) = f(x_2) \qquad \Leftrightarrow \qquad x_2 = s \oplus x_1 \end{aligned}$$

In other words, regardless of what $f(x)$ does behind the scenes, its output is the same for inputs $x_1$ and $x_2$ if and only if $x_2 = s \oplus x_1$, or, equivalently, $x_1 = s \oplus x_2$.

The goal is to find the $n$-bit number $s$, using as few calls to $f$ as possible. There are two cases: if $s = 0$, then $f$ is one-to-one, since $x_2 = 0 \oplus x_1 = x_1$. Otherwise, if $s \neq 0$, then $f$ is two-to-one by definition: for every $x_1$ there exists exactly one $x_2$ such that $x_2 = s \oplus x_1$.

A classical computer solves this by randomly guessing inputs, until it finds two that give the same output, and then $s = x_1 \oplus x_2$. For $n$-bit numbers, this takes $\mathcal{O}(\sqrt{2^n})$ guesses (the square root is due to the birthday paradox).

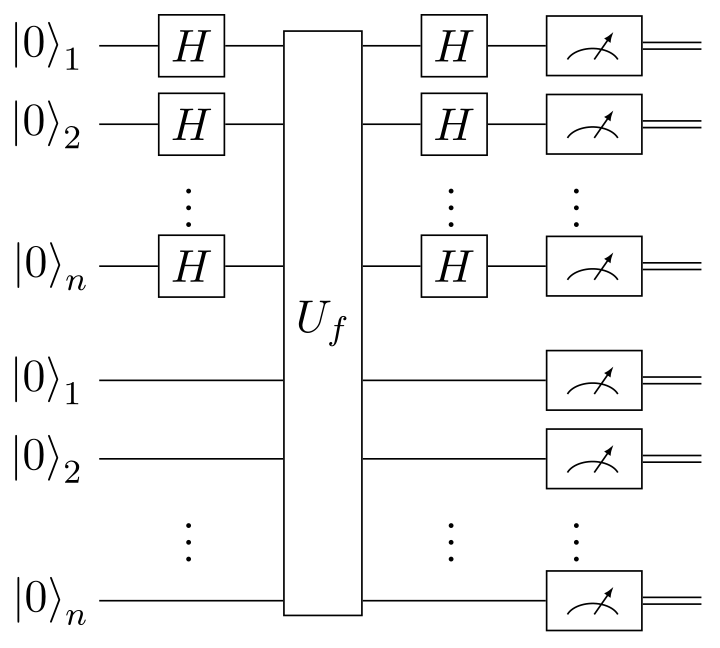
A quantum computer needs to query $f$ only $\mathcal{O}(n)$ times, although the exact number varies due to the algorithm’s probabilistic nature. It uses the following circuit:

The XOR oracle $U_f$ implements $f$, and has the following action for $n$-bit $a$ and $b$:

$$\begin{aligned} \Ket{a} \Ket{b} \quad \to \boxed{U_f} \to \quad \Ket{a} \Ket{b \oplus f(a)} \end{aligned}$$

Starting from the state $\Ket{0}^{\otimes 2 n}$, we apply the Hadamard gate $H$ to each of the first $n$ qubits:

$$\begin{aligned} \Ket{0}^{\otimes n} \Ket{0}^{\otimes n} \quad \to \boxed{H^{\otimes n}} \to \quad \Ket{+}^{\otimes n} \Ket{0}^{\otimes n} = \frac{1}{\sqrt{2^n}} \sum_{x = 0}^{2^n - 1} \Ket{x} \Ket{0}^{\otimes n} \end{aligned}$$

Where $\Ket{x}$ is shorthand for $\Ket{x}_1 \cdots \Ket{x}_n$. In other words, we now have an equal superposition of all possible inputs $x$, with a constant $\Ket{0}^{\otimes n}$ beside it. We give this to the oracle $U_f$:

$$\begin{aligned} \frac{1}{\sqrt{2^n}} \sum_{x = 0}^{2^n - 1} \Ket{x} \Ket{0}^{\otimes n} \quad \to \boxed{U_f} \to \quad \frac{1}{\sqrt{2^n}} \sum_{x = 0}^{2^n - 1} \Ket{x} \Ket{f(x)} \end{aligned}$$

Then we apply $H^{\otimes n}$ to the first $n$ qubits again, which, thanks to the definition of the Hadamard transform, yields the following, where $x \cdot y$ is the bitwise dot product:

$$\begin{aligned} \frac{1}{\sqrt{2^n}} \sum_{x = 0}^{2^n - 1} \Ket{x} \Ket{f(x)} \quad \to \boxed{H^{\otimes n}} \to \quad &\frac{1}{\sqrt{2^n}} \sum_{x = 0}^{2^n - 1} \bigg( \frac{1}{\sqrt{2^n}} \sum_{y = 0}^{2^n - 1} (-1)^{x \cdot y} \Ket{y} \bigg) \Ket{f(x)} \end{aligned}$$

Next, we measure all qubits. The order in which we do this does not matter, but, for clarity, let us measure the last $n$ qubits first, yielding $\Ket{f(x_1)}$ for some $x_1$. Doing this leaves the $2n$ qubits in the following state, where $f(x_1) = f(x_2)$ and $x_2 = s \oplus x_1$:

$$\begin{alignedat}{2} &\mathrm{if} \: s = 0: \qquad &&\bigg( \frac{1}{\sqrt{2^{n}}} \sum_{y = 0}^{2^n - 1} (-1)^{x_1 \cdot y} \Ket{y} \bigg) \Ket{f(x_1)} \\ &\mathrm{if} \: s \neq 0: \qquad &&\bigg( \frac{1}{\sqrt{2^n}} \sum_{y = 0}^{2^n - 1} \frac{1}{\sqrt{2}} \Big( (-1)^{x_1 \cdot y} + (-1)^{x_2 \cdot y} \Big) \Ket{y} \bigg) \Ket{f(x_1)} \end{alignedat}$$

If $s = 0$, we get an equal superposition of all $y$, so when we measure the first $n$ qubits, the result is a uniformly random number, regardless of the phase $(-1)^{x_1 \cdot y}$.

If $s \neq 0$, we get an “extra superposition”, since $x_1 \neq x_2$ but both are candidate inputs. This is a more interesting situation, because we can only measure $y$-values where:

$$\begin{aligned} 0 \neq (-1)^{x_1 \cdot y} + (-1)^{x_2 \cdot y} \end{aligned}$$

Since $x_2 = s \oplus x_1$ by definition, we can rewrite this as follows:

$$\begin{aligned} 0 \neq (-1)^{x_1 \cdot y} + (-1)^{x_1 \cdot y \oplus s \cdot y} = (-1)^{x_1 \cdot y} + (-1)^{x_1 \cdot y} (-1)^{s \cdot y} \end{aligned}$$

Clearly, this expression can only be nonzero if $s \cdot y$ is even. In other words, when we measure the first $n$ qubits, we get a random $y$-value, for which $s \cdot y$ is guaranteed to be even.

In both cases $s = 0$ and $s \neq 0$, measuring the first $n$ qubits gives a $y$-value satisfying:

$$\begin{aligned} s \cdot y = 0 \:\bmod 2 \end{aligned}$$

This tells us something about $s$, albeit not much. But if we run Simon’s algorithm $N$ times, we get various $y$-values $y_1, ..., y_N$, from which we can build a system of linear equations:

$$\begin{aligned} s \cdot y_1 &= 0 \:\bmod 2 \\ s \cdot y_2 &= 0 \:\bmod 2 \\ &\:\:\vdots \\ s \cdot y_N &= 0 \:\bmod 2 \end{aligned}$$

This can be solved efficiently by a classical computer. In the best-case scenario, all those $y$-values would be linearly independent (when regarded as vectors of bits), in which case only $N = n - 1$ equations would be necessary. Simon’s algorithm is therefore $\mathcal{O}(n)$.

It may feel like “cheating” to use a classical computer at the end. Remember that the point of this algorithm is to limit the number of oracle queries, which we did successfully. Querying an oracle might be a very expensive operation, so that is a big improvement! That said, Simon’s algorithm currently has no known practical uses.

References

1. J.S. Neergaard-Nielsen, Quantum information: lectures notes, 2021, unpublished.
2. S. Aaronson, Introduction to quantum information science: lecture notes, 2018, unpublished.

---